Bài 1: Tính B = 1 + 2 + 3 +...+ 98 + 99
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


55 + 88 = 143
143 = ... + 90
... = 143 - 90
... = 53
Vậy 55 + 88 = 53 + 90 = 143

Với $x>0;x\ne1$:
$P=\frac{\sqrt x+1}{\sqrt x-1}+\frac{2\sqrt x+1}{x-\sqrt x}+\frac{1}{\sqrt x}$
$=\frac{\sqrt x\left(\sqrt x+1\right)}{\sqrt x\left(\sqrt x-1\right)}+\frac{2\sqrt x+1}{\sqrt x\left(\sqrt x-1\right)}+\frac{\sqrt x-1}{\sqrt x\left(\sqrt x-1\right)}$
$=\frac{x+\sqrt x+2\sqrt x+1+\sqrt x-1}{\sqrt x\left(\sqrt x-1\right)}$
$=\frac{x+4\sqrt x}{\sqrt x\left(\sqrt x-1\right)}=\frac{\sqrt x\left(\sqrt x+4\right)}{\sqrt x\left(\sqrt x-1\right)}=\frac{\sqrt x+4}{\sqrt x-1}$
$Toru$

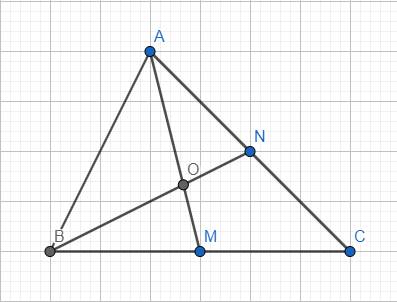
\(\text{△ABC}\) có: \(AM,BN\) là 2 đường trung tuyến (gt)
Mà \(O\) là giao điểm của \(AM\) và \(BN\) nên:
\(O\) là trọng tâm của \(\text{△ABC}\)
\(\Rightarrow ON=\dfrac{1}{2}OB\) (theo tính chất ba đường trung tuyến trong tam giác)
Thay \(ON=1\) được:
\(OB=2\cdot ON=2\cdot1=2\)
Vậy \(OB=2\)
Vì ON = 1 , và O là trọng tâm, thì OB sẽ là 2 lần ON , tức là:
OB = 2 x ON = 2 x 1 = 2
Vậy độ dài của OB là 2.

Ta có hệ phương trình: a^3 - 3ab^2 = 2,b^3 - 3a^2b = -11
Cộng hai phương trình với nhau ta được:
a^3 - 3ab^2 + b^3 - 3a^2b
= 2 - 11,(a^3 + b^3) - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2) - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2 - 3ab)
= -9,(a + b)(a^2 - 4ab + b^2) = -9
Ta cần tìm giá trị của a^2 + b^2. Ta có:,(a + b)^2 = a^2 + b^2 + 2ab
Vậy:,a^2 + b^2 = (a + b)^2 - 2ab
Ta có:,a^3 - 3ab^2 = 2,b^3 - 3a^2b = -11
Cộng hai phương trình ta được:
a^3 + b^3 - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2) - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2 - 3ab)
= -9,(a + b)(a^2 - 4ab + b^2) = -9
Thay a^2 - 4ab + b^2 = -9 vào phương trình (a + b)(a^2 - 4ab + b^2) = -9 ta được:
(a + b)(-9) = -9,a + b = 1
Thay a + b = 1 vào công thức a^2 + b^2 = (a + b)^2 - 2ab
Ta được:,a^2 + b^2 = 1^2 - 2ab,a^2 + b^2 = 1 - 2ab
Vậy để tính a^2 + b^2, chúng ta cần tìm giá trị của ab.
Thay a + b = 1 vào a^3 - 3ab^2 = 2 ta được:
a^3 - 3ab^2 =
2,a^3 - 3a(1 - a)^2
= 2,a^3 - 3a(1 - 2a + a^2)
= 2,a^3 - 3a + 6a^2 - 3a^3
= 2,-2a^3 + 6a^2 - 3a - 2
= 0,2a^3 - 6a^2 + 3a + 2
= 0,2(a^3 - 3a^2 + 3a - 1)
= 0,2(a - 1)^3 = 0
Vậy a = 1 hoặc a = b
Nếu a = 1, ta có:
1 - 3b^2 = 2,-3b^2 = 1,b^2 = -1, không có giá trị thực cho b.
Nếu a = b, ta có:,a^3 - 3a^3 = 2,-2a^3 = 2,a^3 = -1,a = -1
Vậy a = -1, b = -1
Thay a = -1, b = -1 vào a^2 + b^2 = 1 - 2ab ta được:
a^2 + b^2 = 1 - 2(-1)(-1) = 1 - 2 = -1
Vậy kết quả là a^2 + b^2 = -1.

I,II,III,IV,V,VI,VII,VIII,IX,X,XI,XII,XIII,XIV,XV,XVI,XVII,XVII,XVIII,XIX,XX

Bài 2:
a: \(\sqrt{\left(2x-1\right)^2}=4\)
=>|2x-1|=4
=>\(\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
b: ĐKXĐ: x>=-1
\(\sqrt{4x+4}-\sqrt{9x+9}-8\sqrt{\dfrac{x+1}{16}}=5\)
=>\(2\sqrt{x+1}-3\sqrt{x+1}-8\cdot\dfrac{\sqrt{x+1}}{4}=5\)
=>\(-3\sqrt{x+1}=5\)
=>\(\sqrt{x+1}=-\dfrac{5}{3}\)(vô lý)
=>Phương trình vô nghiệm
Bài 3:
a: \(Q=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}+1}-\dfrac{2}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}+1}-\dfrac{2}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-2\left(\sqrt{x}-1\right)-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+\sqrt{x}-2\sqrt{x}+2-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
b: Thay x=9 vào Q, ta được:
\(Q=\dfrac{3}{3+1}=\dfrac{3}{4}\)
Bài 4:
\(\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}\)
\(=\sqrt{x-1-2\sqrt{x-1}+1}+\sqrt{x-1+2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}\)
\(=\sqrt{x-1}-1+\sqrt{x-1}+1\left(x>=2\right)\)
\(=2\sqrt{x-1}\)


Em nên viết bằng công thức toán học có biểu tượng Σ góc trái màn hình em nhé. Như vậy mọi người mới hiểu đúng đề được để có thể hỗ trợ tốt nhất cho em.

Ta có: a/b=15/21=5/7; b/c=9/12=3/4
Đặt a/b=5k/7k
b/c=3k1/4k1
c/d=9k2/11k2
Điều kiện là k, k1; k2 thuộc N*
Khi đó:
+ b=7k=3k1
Vì b là số tự nhiên suy ra 3k1 chia hết cho 7
Do 3 và 7 là hai số đôi một nguyên tố cùng nhau nên k1 chia hết cho 7
+ c=4k1=9k2
Vì c là số tự nhiên suy ra 4k1 chia hết cho 9
Do 9 và 4 là hai số nguyên tố cùng nhau suy ra k1 chia hết cho 9
Ta thấy: K1 là nhỏ nhất và khác 0
Mà k1 chia hết cho cả 7 và 9 suy ra k1=63
Suy ra b=63x3=189
a= 189:7x5=135
c= 63x4=252
d=252:9x11=308

Dấu âm đó là dấu âm của tử thôi bạn. Và vì mẫu số phải đáp ứng điều kiện là `<0` để là một phân số, nên nếu mẫu số có dấu âm sẽ được chuyển lên tử nhé! Nếu cả 2 đều chứa dấu âm thì phân số đó dương.
Ta có công thức luỹ thừa của một số hữu tỉ như sau:
(\(\dfrac{a}{b}\))m = \(\dfrac{a^m}{b^m}\) (a; b; m \(\in\) Z; b ≠ 0)
Áp dụng với ( \(\dfrac{-1}{2}\) )7 ta có a = -1; b = 2; m = 7
Khi đó: (\(\dfrac{-1}{2}\))7 = \(\dfrac{\left(-1\right)^7}{\left(2\right)^7}\) = \(\dfrac{-1}{128}\)

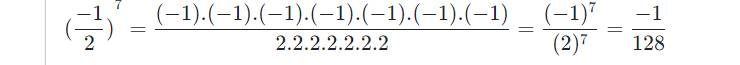
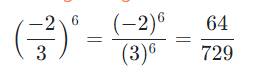
`#3107.101107`
`1.`
Số hạng của tổng B:
`(99 - 1) \div 1 + 1 = 99` (số hạng)
Giá trị của tổng B:
`(99 + 1) \cdot 99 \div 2 = 4950`