Một cây tre cao 8m bị gãy ngang thân, ngọn cây chạm đất cách gốc 4m. Hỏi độ dài từ điểm gãy tới gốc?
#Toán lớp 7Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
Tổng hai số lớn hơn số hạng thứ nhất 345 đơn vị nên số hạng thứ hai là 345.
Số hạng thứ nhất là:
\(345+77=422\)
Tổng hai số đó là:
\(422+345=767\)
Đáp số: 767
Bài 4:
Hiệu phép trừ đó là:
\(168+77=245\)
Số trừ là:
\(245-77=168\)
Số bị trừ trong phép trừ đó là:
\(245+168=413\)
Đáp số: 413

Bài 1:
Hiệu số gạo bác Tùng mua và số gạo bác Hai mua là:
\(19-4=15\left(kg\right)\)
Số gạo bác Tùng mua là:
\(345+15=360\left(kg\right)\)
Số gạo bác Hà mua là:
\(345-7=338\left(kg\right)\)
Đáp số: Bác Hai: 345 kg
Bác Tùng: 360 kg
Bác Hà: 338 kg
Bài 2:
Nếu ba ngày đều bán được 288 lít thì cửa hàng nhập về số lít bia là:
\(288\cdot3=864\left(l\right)\)
Cửa hàng nhập về số lít bia là:
\(864-29+\left(37-29\right)=843\left(l\right)\)
Đáp số: 843 l

\(\left(4x-5\right)\left(\dfrac{5}{4}x-2\right)=1\dfrac{1}{3}\)
=>\(5x^2-8x-\dfrac{25}{4}x+10-\dfrac{4}{3}=0\)
=>\(5x^2-\dfrac{57}{4}x+\dfrac{26}{3}=0\)
\(\Delta=\left(-\dfrac{57}{4}\right)^2-4\cdot5\cdot\dfrac{26}{3}=\dfrac{1427}{48}>0\)
=>Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{\dfrac{57}{4}-\sqrt{\dfrac{1427}{48}}}{2\cdot5}=\dfrac{\dfrac{57}{4}-\dfrac{\sqrt{4281}}{12}}{10}=\dfrac{171-\sqrt{4281}}{120}\\x=\dfrac{171+\sqrt{4281}}{120}\end{matrix}\right.\)

1) Ta có: \(B=2019\times2022\)
\(=\left(2020-1\right)\times\left(2021+1\right)\)
\(=\left(2020-1\right)\times2021+\left(2020-1\right)\)
\(=2020\times2021-2021+2020-1\)
\(=2020\times2021-2\)
\(< 2020\times2021=A\)
Vậy \(B< A\)
2) Điều đó không thể xảy ra được, vì nếu gọi 7 số chưa biết theo thứ tự là \(a,b,c,d,e,f,g\) và tổng 3 số ở 3 ô bất kì bằng 17 thì phải có:
\(a+b+4=a+b+c=a+b+d=a+b+e=...=a+b+8\)
Vậy thì rõ ràng vô lí vì từ chỗ này suy ra \(4=8\left(??\right)\)
Nên bạn xem lại đề nhé.

Lời giải:
Ta có:
$P(1)=(2.1-1)^6+(1-2)^7=a_7.1^7+a_6.1^6+....+a_1.1+a_0$
$\Rightarrow 1+(-1)=a_7+a_6+a_5+....+a_1+a_0$
$\Rightarrow a_7+a_6+a_5+....+a_1+a_0=0$

Lời giải:
Ta có:
$P(1)=(2.1-1)^6+(1-2)^7=a_7.1^7+a_6.1^6+....+a_1.1+a_0$
$\Rightarrow 1+(-1)=a_7+a_6+a_5+....+a_1+a_0$
$\Rightarrow a_7+a_6+a_5+....+a_1+a_0=0$

Lời giải:
$a+b+c=0\Rightarrow a+b=-c$. khi đó:
$a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3=(-c)^3-3ab(-c)+c^3$
$=-c^3+3abc+c^3=3abc$
Ta có đpcm.
ta có: a+b+c=0
=> c=-(a+b)
ta thay vào biểu thức:
=>a3+b3-(a+b)3=3ab(-a-b)
=>-3a2b-3ab2=-3a2b-3ab2
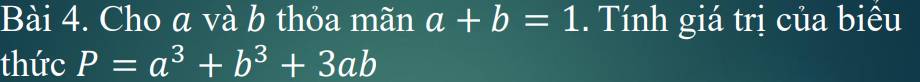

Lời giải:
Ký hiệu gốc cây là $A$, ngọn cây bị gãy là $B$, điểm gãy là $C$. Ta có:
$AC+CB=8(1)$ (m)
$AB=4$ (m)
Áp dụng định lý Pitago:
$AC^2+AB^2=BC^2$
$\Rightarrow AC^2+4^2=BC^2$
$\Rightarrow BC^2-AC^2=16$
$\Rightarrow (BC-AC)(BC+AC)=16$
$\Rightarrow (BC-AC).8=16\Rightarrow BC-AC=2(2)$
Từ $(1); (2)\Rightarrow BC=(8+2):2=5; AC=(8-2):2=3$ (m)
Vậy độ dài từ điểm gãy tới gốc là $AC=3$ m
Hình vẽ: