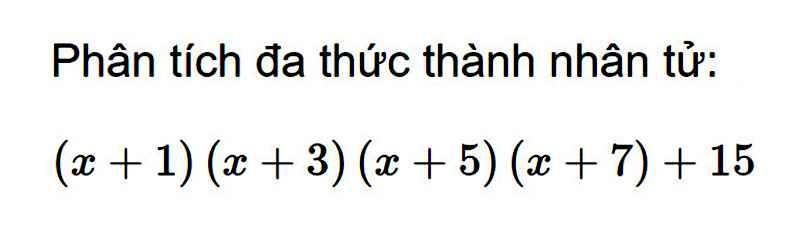
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2x³ - 5x² + 8x - 3
= 2x³ - x² - 4x² + 2x + 6x - 3
= (2x³ - x²) - (4x² - 2x) + (6x - 3)
= x²(2x - 1) - 2x(2x - 1) + 3(2x - 1)
= (2x - 1)(x² - 2x + 3)

a: ĐKXĐ: \(x\notin\left\{0;2\right\}\)
b: \(C=\dfrac{x^2}{x-2}\cdot\left(\dfrac{x^2+4}{x}-4\right)+3\)
\(=\dfrac{x^2}{x-2}\cdot\dfrac{x^2-4x+4}{x}+3\)
\(=\dfrac{x^2\left(x-2\right)^2}{x\left(x-2\right)}+3=x\left(x-2\right)+3=x^2-2x+3\)

=2x1x3x21+2x2x3x31+2x3x3x41+...+2x18x3x191+2x19x3x201=
=12𝑥3𝑥(11𝑥2+12𝑥3+13𝑥4+...+118𝑥19+119𝑥20)==2x31x(1x21+2x31+3x41+...+18x191+19x201)=
=16𝑥(2−11𝑥2+3−22𝑥3+4−33𝑥4+...+20−1919𝑥20)==61x(1x22−1+2x33−2+3x44−3+...+19x2020−19)=
=16𝑥(1−12+12−13+13−14+...+119−120)==61x(1−21+21−31+31−41+...+191−201)=
=16𝑥(1−120)=16𝑥1920=19120=61x(1−201)=61x2019=12019


a: \(S_{ABC}=3\times S_{BCE}\)
=>\(S_{BCE}=\dfrac{45}{3}=15\left(cm^2\right)\)
=>\(S_{ABE}=45-15=30\left(cm^2\right)\)

\(T=\left\{5;7;9;...;85;87\right\}\)
Gọi \(a\) là phần tử thứ 13 tính từ trái sang phải
\(\Rightarrow\left(a-5\right):2+1=13\)
\(\Rightarrow\left(a-5\right):2=13-1\)
\(\Rightarrow\left(a-5\right):2=12\)
\(\Rightarrow a-5=12\times2\)
\(\Rightarrow a-5=24\)
\(\Rightarrow a=24+5\)
\(\Rightarrow a=29\)
Vậy phần tử thứ 13 tính từ trái sang phải là 29

\(x^2-x\left(m+2\right)+2m=0\)
De pt co 2 nghiem phan biet khi delta > 0
\(\Delta=\left(m+2\right)^2-4.2m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Ma (m-2)^2 >= 0 voi moi x
=> m - 2 \(\ne0\Rightarrow m\ne2\)
\(x^2-2x-mx+2m=0\)
\(x^2-\left(2+m\right)x+2m=0\)
\(\Delta=\left[-\left(2+m\right)\right]^2-4.1.2m\)
\(=4+4m+m^2-8m\)
\(=m^2-4m+4\)
\(=\left(m-2\right)^2\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\left(m-2\right)^2>0\)
\(m-2\ne0\)
\(m\ne2\)
Vậy \(m\ne2\) thì phương trình đã cho có hai nghiệm phân biệt







`(x+1)(x+3)(x+5)(x+7)+15`
`=(x+1)(x+7)(x+3)(x+5)+15`
`= (x^2+7x+x+7)(x^2+5x+3x+15)+15 `
`=(x^2 +8x+7)(x^2+8x+15)+15`
Đặt `t=x^2 +8x+11`
`=(t-4)(t+4)+15`
`=t^2 -16 +15`
`=t^2 -1`
`=(t-1)(t+1)`
`=(x^2 +8x+11-1)(x^2 +8x+11+1)`
`=(x^2 +8x+10)(x^2 +8x+12)`