S=5+5^2+5^3+5^4+...+5^2019 chứng minh S chia hết cho 21
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAPE vuông tại P và ΔAPH vuông tại P có
AP chung
PE=PH
Do đó: ΔAPE=ΔAPH
Xét ΔAQH vuông tại Q và ΔAQF vuông tại Q có
AQ chung
QH=QF
Do đó; ΔAQH=ΔAQF
b: ΔAPE=ΔAPH
=>\(\widehat{PAE}=\widehat{PAH}\)
=>AP là phân giác của góc HAE
ΔAQH=ΔAQF
=>\(\widehat{QAH}=\widehat{QAF}\)
=>AQ là phân giác của góc HAF
\(\widehat{EAF}=\widehat{EAH}+\widehat{FAH}\)
\(=2\widehat{QAH}+2\cdot\widehat{PAH}=2\cdot\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot\widehat{QAP}=180^0\)
=>E,A,F thẳng hàng

Bài 6: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{142^0}{2}=71^0\)
Ta có: \(\widehat{xOz}+\widehat{x'Oz}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oz}+71^0=180^0\)
=>\(\widehat{x'Oz}=109^0\)
Bài 7:
Ta có: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}=90^0\)
Ot là phân giác của góc xOz
=>\(\widehat{zOt}=\dfrac{\widehat{xOz}}{2}=\dfrac{90^0}{2}=45^0\)
Ov là phân giác của góc yOz
=>\(\widehat{vOz}=\dfrac{90^0}{2}=45^0\)
\(\widehat{vOt}=\widehat{zOv}+\widehat{zOt}=45^0+45^0=90^0\)

b: \(\dfrac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}\cdot\dfrac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}=8^x\)
=>\(8^x=\dfrac{4\cdot4^5}{3\cdot3^5}\cdot\dfrac{6\cdot6^5}{2\cdot2^5}\)
=>\(8^x=\dfrac{4^6}{2^6}\cdot\dfrac{6^6}{3^6}=2^6\cdot2^6=2^{12}=\left(2^3\right)^4=8^4\)
=>x=4

1: \(5^{x+4}-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(5^{x+3}\cdot5-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(2\cdot5^{x+3}=2\cdot5^{11}\)
=>x+3=11
=>x=8
2: \(\dfrac{1}{2}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\cdot\left(\dfrac{1}{2}+4\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=2^6\)
=>x=6
3: \(9^{2x+1}=27^3\)
=>\(3^{4x+2}=3^9\)
=>4x+2=9
=>4x=7
=>\(x=\dfrac{7}{4}\)
4: \(2^{-1}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\left(4+\dfrac{1}{2}\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=9\cdot2^5:\dfrac{9}{2}=2^6\)
=>x=6
5: \(\left(2x-1\right)^3=\dfrac{8}{27}\)
=>\(\left(2x-1\right)^3=\left(\dfrac{2}{3}\right)^3\)
=>\(2x-1=\dfrac{2}{3}\)
=>\(2x=\dfrac{2}{3}+1=\dfrac{5}{3}\)
=>\(x=\dfrac{5}{3}:2=\dfrac{5}{6}\)

Gọi số điểm cho trước là x(điểm)
(Điều kiện: \(x\in Z^+;x>3\))
Số điểm không thẳng hàng là x-3(điểm)
TH1: vẽ 1 đường thẳng đi qua 3 điểm thẳng hàng
=>Có 1 đường thẳng
TH2: Chọn 2 điểm bất kì trong x-3 điểm còn lại
Số đường thẳng là \(C^2_{x-3}=\dfrac{\left(x-3\right)!}{\left(x-3-2\right)!\cdot2!}=\dfrac{\left(x-4\right)\left(x-3\right)}{2}\)(đường)
TH3: Chọn 1 điểm trong 3 điểm thẳng hàng, 1 điểm trong x-3 điểm còn lại
=>Có 3(x-3) đường thẳng
Tổng số đường thẳng là 120 đường nên ta có:
\(1+\dfrac{\left(x-4\right)\left(x-3\right)}{2}+3\left(x-3\right)=120\)
=>\(\dfrac{2+\left(x-4\right)\left(x-3\right)+6\left(x-3\right)}{2}=120\)
=>2+(x-4)(x-3)+6(x-3)=240
=>\(2+x^2-7x+12+6x-18=240\)
=>\(x^2-x-244=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{1+\sqrt{977}}{2}\left(loại\right)\\x=\dfrac{1-\sqrt{977}}{2}\left(loại\right)\end{matrix}\right.\)

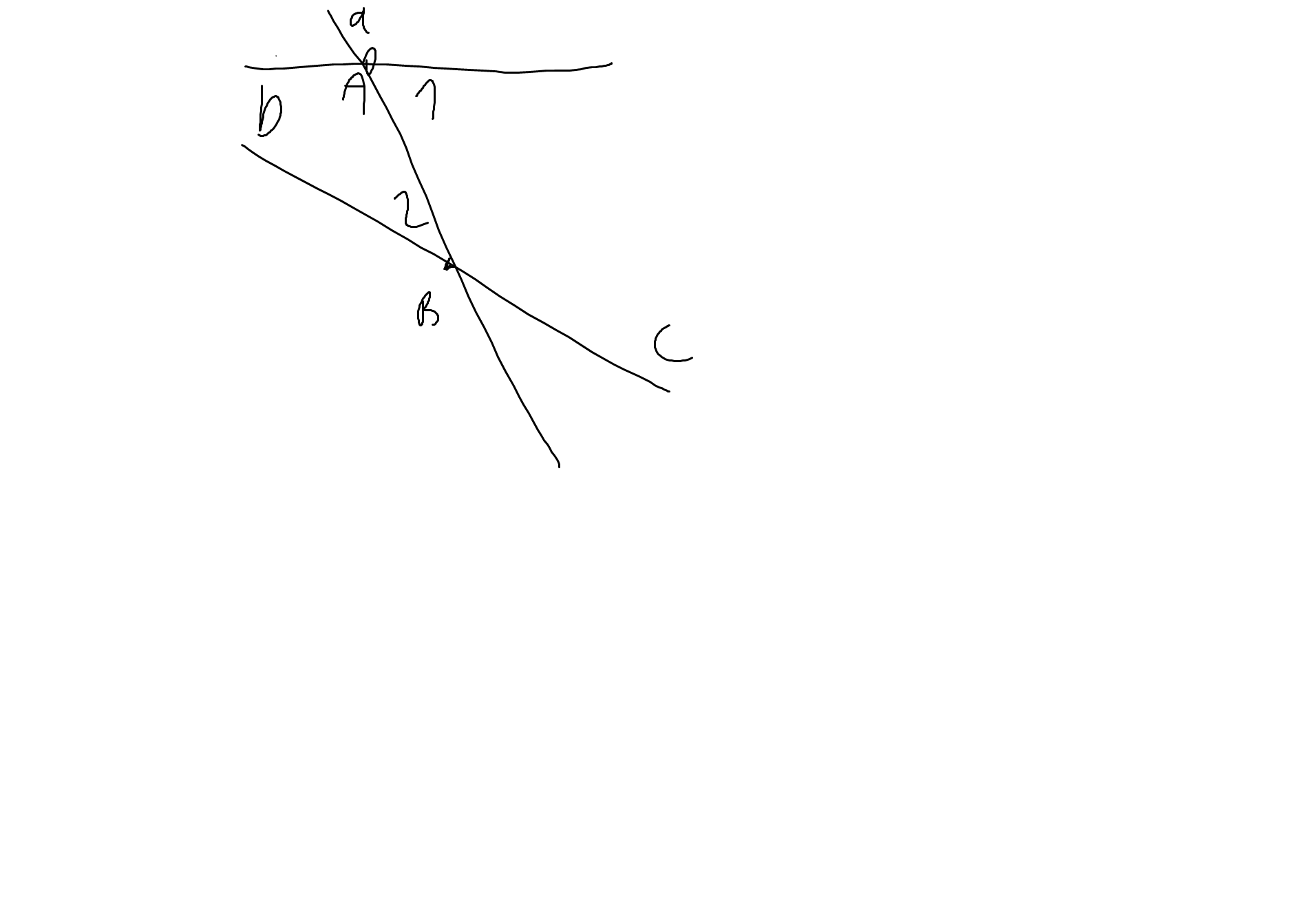
| GT | a cắt b tại A, a cắt c tại B \(\widehat{A_1}\ne\widehat{B_2}\) |
| KL | b cắt c |
Vì \(\widehat{A_1}\ne\widehat{B_2}\)
nên b sẽ không song song với c
mà b và c là hai đường thẳng phân biệt
nên b cắt c

\(\left(\dfrac{1}{6}+\dfrac{1}{3}\right)^2:\left(1+\dfrac{2}{3}-\dfrac{5}{4}\right)\)
\(=\left(\dfrac{1}{6}+\dfrac{2}{6}\right)^2:\left(\dfrac{12}{12}+\dfrac{8}{12}-\dfrac{15}{12}\right)\)
\(=\left(\dfrac{3}{6}\right)^2:\dfrac{5}{12}=\dfrac{1}{4}\cdot\dfrac{12}{5}=\dfrac{3}{5}\)

Sửa đề: x-2y+3z=-33
10x=6y=5z
=>\(\dfrac{10x}{30}=\dfrac{6y}{30}=\dfrac{5z}{30}\)
=>\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}\)
mà x-2y+3z=-33
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x-2y+3z}{3-2\cdot5+3\cdot6}=\dfrac{-33}{11}=-3\)
=>\(x=-3\cdot3=-9;y=-3\cdot5=-15;z=-3\cdot6=-18\)

\(\widehat{zOn}-\dfrac{1}{2}\cdot\widehat{yOn}\)
\(=90^0-\widehat{zOm}-\dfrac{1}{2}\left(180^0-\widehat{xOn}\right)\)
\(=90^0-\widehat{zOm}-90^0+\dfrac{1}{2}\cdot\widehat{xOn}\)
\(=\dfrac{1}{2}\cdot\widehat{xOn}-\widehat{zOm}=\dfrac{1}{2}\left(\widehat{xOn}-\widehat{xOm}\right)=\dfrac{1}{2}\cdot\widehat{nOm}=45^0\)


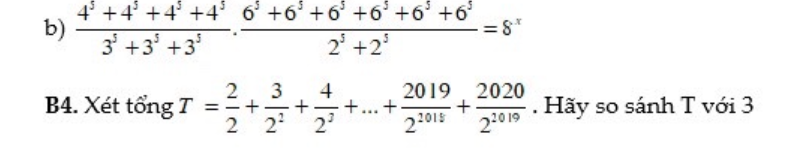
sửa đề chia hết 31 nhé
\(S=5+5^2+5^3+...+5^{2019}=5\left(1+5+5^2+5^3\right)+...+5^{2016}\left(1+5+5^2+5^3\right)\)
\(=31\left(5+...+5^{2016}\right)⋮31\)
Vậy ta có đpcm