Điểm M là trung điểm của BC nên \(MC=MB=\dfrac{1}{2}BC\) 

Mà: \(AM=\dfrac{1}{2}BC\left(gt\right)\)

\(\Rightarrow AM=MC=MB\)

\(\Rightarrow\Delta AMB\) cân tại M (vì AM = MB) 

\(\Rightarrow\widehat{ABC}=\widehat{MAB}\) (hai góc ở đáy) 

Tương tự ta có: \(\widehat{BCA}=\widehat{MAC}\)

Mà: \(\widehat{ABC}+\widehat{BCA}+\widehat{BAC}=180^o\)

\(\Rightarrow\widehat{MAB}+\widehat{MAC}+\widehat{BAC}=180^o\)

\(\Rightarrow2\widehat{BAC}=180^o\)

\(\Rightarrow\widehat{BAC}=90^o\)

Cho tam giác ABC ,M là trung điểm của BC , biết AM = 1/2 BC . Chứng minh tam giác ABC vuông tại A

Bạn tìm kiếm học liệu trên olm nhé, đã có nhiều bạn hỏi r nha

Sửa đề bài: Tìm x nguyển để các biểu thức đó nguyên: 

Ta có:

\(A=\dfrac{x-13}{x-4}=\dfrac{x-4-9}{x-4}=\dfrac{x-4}{x-4}-\dfrac{9}{x-4}=1-\dfrac{9}{x-4}\)

Để A nguyên thì \(\dfrac{9}{x-4}\) phải nguyên 

\(\Rightarrow9\) ⋮ x - 4

\(\Rightarrow x-4\inƯ\left(9\right)=\left\{1;-1;3;-3;9;-9\right\}\)

\(\Rightarrow x\in\left\{5;3;7;1;13;-5\right\}\)

_____________

Ta có:

\(B=\dfrac{5x+1}{x+2}=\dfrac{5x+10-9}{x+2}=\dfrac{5\left(x+2\right)-9}{x+2}=5-\dfrac{9}{x+2}\)

Để B nguyên thì \(\dfrac{9}{x+2}\) phải nguyên: 

\(\Rightarrow9\) ⋮ x + 2

\(\Rightarrow x+2\inƯ\left(9\right)=\left\{1;-1;3;-3;9;-9\right\}\)

\(\Rightarrow x\in\left\{-1;-3;1;-5;7;-11\right\}\)

a) Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{16}{8}=2\)

Do đó:

\(\dfrac{x}{3}=2\Rightarrow x=3.2=6\)

\(\dfrac{y}{5}=2\Rightarrow y=5.2=10\)

Vậy x = 6; y = 10.

b) Ta có: \(x:2=y:\left(-5\right)=\dfrac{x}{2}=\dfrac{y}{-5}\)

Áp dụng TCDTSBN, ta có: 

\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=-\dfrac{7}{7}=-1\)

Do đó:

\(\dfrac{x}{2}=-1\Rightarrow x=2.\left(-1\right)=-2\)

\(\dfrac{y}{-5}=-1\Rightarrow y=\left(-5\right).\left(-1\right)=5\)

Vậy x = -2; y = 5.

Lời giải:
$T = \frac{1}{7^2}+\frac{2}{7^3}+\frac{3}{7^4}+....+\frac{99}{7^{100}}$
$7T = \frac{1}{7}+\frac{2}{7^2}+\frac{3}{7^3}+....+\frac{99}{7^{99}}$

$\Rightarrow 6T=7T-T = \frac{1}{7}+\frac{1}{7^2}+\frac{1}{7^3}+...+\frac{1}{7^{99}}-\frac{99}{7^{100}}$
$42T = 1+\frac{1}{7}+\frac{1}{7^2}+...+\frac{1}{7^{98}}-\frac{99}{7^{99}}$

$\Rightarrow 42T-6T = 1-\frac{100}{7^{99}}+\frac{99}{7^{100}}$

$\Rightarrow 36T = 1-\frac{601}{7^{100}}< 1$

$\Rightarrow T< \frac{1}{36}$

\(\dfrac{2^{12}.3^5-2^{12}.3^6}{2^{12}.9^3+8^4.3^5}=\dfrac{2^{12}.\left(3^5-3^6\right)}{2^{12}.\left(3^2\right)^3+\left(2^3\right)^4.3^5}\\ =\dfrac{2^{12}.\left(3^5-3^6\right)}{2^{12}.\left(3^6+3^5\right)}=\dfrac{3^5-3^6}{3^6+3^5}\\ =\dfrac{3^5\left(1-3\right)}{3^5\left(1+3\right)}=\dfrac{-2.3^5}{4.3^5}=\dfrac{-2}{4}=-\dfrac{1}{2}\)

Do \(2p+1\) luôn lẻ \(\Rightarrow k^3\) lẻ \(\Rightarrow k\) lẻ \(\Rightarrow k=2n+1\) với n là số tự nhiên

\(\Rightarrow2p+1=\left(2n+1\right)^3\)

\(\Rightarrow2p=\left(2n+1\right)^3-1\)

\(\Rightarrow2p=\left(2n+1-1\right)\left[\left(2n+1\right)^2+2n+1+1\right]\)

\(\Leftrightarrow2p=2n\left(4n^2+6n+3\right)\)

\(\Leftrightarrow p=n\left(4n^2+6n+3\right)\) (1)

Do p nguyên tố \(\Rightarrow p\) chỉ có nhiều nhất 1 ước lớn hơn 1 là chính nó

Do đó (1) thỏa mãn khi và chỉ khi:

\(\left\{{}\begin{matrix}n=1\\p=4n^2+6n+3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}n=1\\p=13\end{matrix}\right.\)

Vậy \(p=13\) là SNT thỏa mãn yêu cầu

Cho M={0,1,4,9}Hỏi M có bao nhiêu tập hợp con A.16B.15C.14D.13

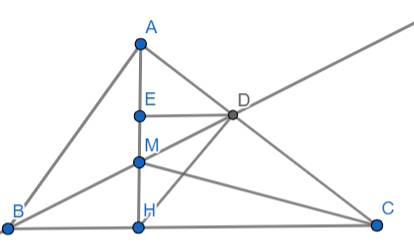
a) Sửa: \(CMR:MB< MC\)

BH là hình chiếu của AB trên BC 

CH là hình chiếu của AC trên BC 

Mà: AB < AC \(\Rightarrow BH< CH\)

BH là hình chiếu của BM trên BC 

CH là hình chiếu của CM trên BC 

Mà: \(BH< CH\Rightarrow MB< MC\)

b) Kẻ DE ⊥ AH 

Điểm M là điểm bất kì trên AH nên: \(AM< AH\)

\(\Rightarrow AM-AE< AH-AE\)

\(\Rightarrow ME< HE\)

ME là hình chiếu của MD trên AH 

HE là hình chiếu của HD trên AH 

Mà: ME < HE \(\Rightarrow MD< HD\)

Câu b đề thiếu rồi em, cần biết quan hệ giữa a và b nữa mới tính được

Bài 4:

a; A = \(\dfrac{4a-5b}{6a+b}\); biết \(\dfrac{a}{b}\) = \(\dfrac{2}{3}\)

    \(\dfrac{a}{b}\) = \(\dfrac{2}{3}\) ⇒ a = \(\dfrac{2}{3}\).b

Thay a = \(\dfrac{2}{3}\)b vào biểu thức A ta có:

        A = \(\dfrac{4.\dfrac{2}{3}.b-5.b}{6.\dfrac{2}{3}.b+b}\) 

       A  = \(\dfrac{b.\left(\dfrac{8}{3}-5\right)}{b.\left(4+1\right)}\)

        A  = \(\dfrac{\dfrac{-7}{3}}{5}\)

         A =  \(\dfrac{-7}{15}\)