Hai thư viện có tất cả 15000 cuốn sách. Nếu chuyển từ thư viện thứ nhất sang thư viện thứ hai 3000 cuốn, thì số sách của hai thư viện bằng nhau. Tính số sách lúc đầu ở mỗi thư viện
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2\(xy\) + 6\(x\) - \(y\) = 6
2\(xy\) + 6\(x\) = 6 + \(y\)
\(x\)(2\(y\) + 6) = 6 + \(y\)
\(x\) = (6 + \(y\) ): (2\(y\)+6)
\(x\) \(\in\) Z ⇔ 6 + \(y\) ⋮ 2\(y\) + 6 ⇒ 2.(6+\(y\)) ⋮ 2\(y\) + 6 ⇒ 12 + 2\(y\) ⋮ 2\(y\) + 6
⇒ 2\(y\) + 6 + 6 ⋮ 2\(y\) + 6 ⇒ 6 ⋮ 2\(y\) + 6 ⇒ 3 ⋮ y + 3
Ư(3) = {-3; -1; 1; 3}
Lập bảng ta có:
| \(y+3\) | -3 | -1 | 1 | 3 |
| \(y\) | -6 | -4 | -2 | 0 |
| \(x\) = (6+\(y\)):(2\(y\)+6) | 0 | -1 | 2 | 1 |
Các cặp (\(x;y\)) thỏa mãn đề bài lần lượt là:
(\(x\); \(y\)) = (0; -6); (-1; -4); (2; -2) ; (1; 0)

Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
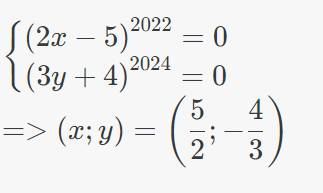 Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)

\(\left[\left(0,1\right)^2\right]^0+\left[\left(\dfrac{1}{7}\right)^{-1}\right]^2\cdot\dfrac{1}{49}\cdot\left[\left(2^2\right)^3:2^5\right]\)
\(=1+7^2\cdot\dfrac{1}{49}\cdot\left(2^6:2^5\right)\)
\(=1+49\cdot\dfrac{1}{49}\cdot2\)
\(=1+1\cdot2\)
\(=3\)

`(4*2^5) \div (2^3*1/6)`
`= (2^2*2^5) \div (8/6)`
`= 2^7 \div 4/3`
`= 96`

\(\left(0,125\right)^3.512=\left(0,125\right)^3.8^3=\left(0,125.8\right)^3=1^3=1\)
\(\left(0,125\right)^3.512\)
\(=\left(0,125\right)^3.8^3\)
\(=\left(0,125\cdot8\right)^3\)
\(=1^3\)
\(=1\)

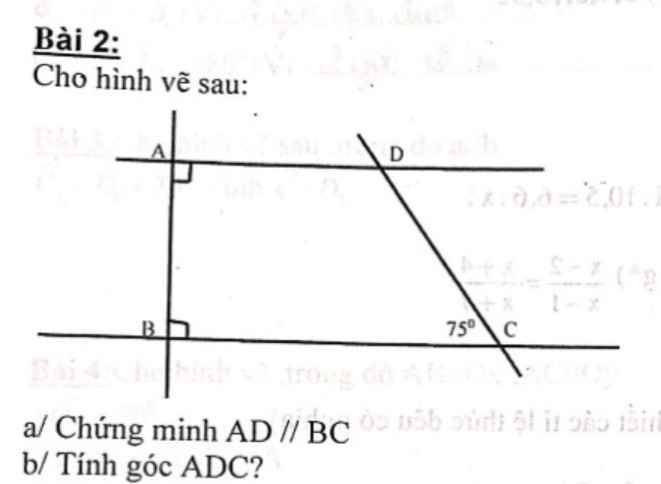
\(a,\) Ta có : \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\BC\perp AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AD//BC\) ( cùng vuông góc với \(AB\) )
\(b,\) Ta có tứ giác thì 4 góc là \(360^o\)
\(\Rightarrow\widehat{ADC}=360^o-\widehat{BAD}-\widehat{ABC}-\widehat{DCB}\)
\(=360^o-90^o-90^o-75^o=105^o\)
Vậy \(\widehat{ADC}=105^o\)
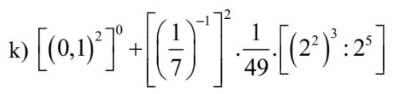
Số sách ở thư viện thứ nhất:
\(\left(15000+3000\right):2=9000\) (cuốn sách)
Số sách ở thư viện thứ hai:
\(15000-9000=6000\) (cuốn sách)
Đáp số:....