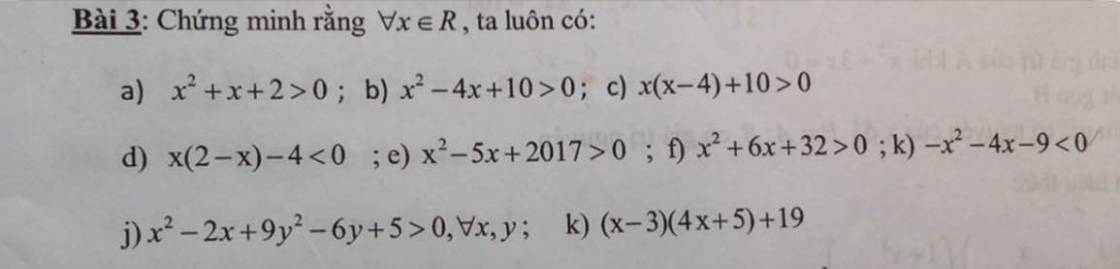Cậu tham khảo nhé !

Điều ước của tôi là trở thành một giáo viên và góp phần lan tỏa tình yêu sách đến với mọi người xung quanh. Tôi luôn tin rằng sách là nguồn tri thức vô tận và có thể mang lại nhiều giá trị cho cuộc sống của con người. Tuy nhiên, không phải ai cũng có cơ hội tiếp cận với sách và hiểu rõ được giá trị của chúng.

Vì vậy, tôi muốn trở thành một giáo viên để giúp đỡ các học sinh yêu thích sách và đọc sách. Tôi muốn khơi dậy niềm đam mê đọc sách cho các em học sinh, giúp các em hiểu rõ hơn về giá trị của việc đọc sách và cách áp dụng kiến thức từ sách vào cuộc sống hàng ngày. Tôi tin rằng việc lan tỏa tình yêu sách sẽ giúp nâng cao tri thức và mang lại lợi ích cho xã hội.

Ngoài ra, tôi cũng mong muốn có thể giúp đỡ những người khác trong việc tiếp cận với sách. Tôi muốn tham gia các hoạt động tình nguyện, tổ chức các lớp học miễn phí hoặc chia sẻ sách cho những người có hoàn cảnh khó khăn. Tôi tin rằng việc này sẽ giúp mọi người có cơ hội tiếp cận với sách và hiểu rõ hơn về giá trị của chúng.

Cuối cùng, tôi muốn truyền cảm hứng cho mọi người xung quanh bằng việc chia sẻ những câu chuyện về sách và những trải nghiệm của bản thân khi đọc sách. Tôi tin rằng việc chia sẻ này sẽ giúp mọi người hiểu rõ hơn về giá trị của sách và có thêm động lực để đọc sách. Tôi hy vọng rằng điều ước của mình sẽ được thực hiện và tôi có thể góp phần lan tỏa tình yêu sách đến với mọi người.

Nguồn : FQA

đkxđ: \(abc\ne0\)

\(a+b+c=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow\left(a+b+c\right)^2=\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\)

 Kết hợp với \(a^2+b^2+c^2=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\) và đẳng thức \(\left(x+y+z\right)^2-\left(x^2+y^2+z^2\right)=2\left(xy+yz+zx\right)\), dễ dàng suy ra \(ab+bc+ca=\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\) \(\Leftrightarrow ab+bc+ca=\dfrac{a+b+c}{abc}\) \(\Leftrightarrow a+b+c=abc\left(ab+bc+ca\right)\) (1)

 Mặt khác, \(a+b+c=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Leftrightarrow a+b+c=\dfrac{ab+bc+ca}{abc}\) \(\Leftrightarrow ab+bc+ca=abc\left(a+b+c\right)\) (2)

Từ (1) và (2), suy ra \(a+b+c=\left(abc\right)^2\left(a+b+c\right)\) \(\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\abc=\pm1\end{matrix}\right.\)

TH1: \(a+b+c=0\), suy ra \(\dfrac{ab+bc+ca}{abc}=0\) hay \(ab+bc+ca=0\), từ đó suy ra \(a^2+b^2+c^2=0\) \(\Leftrightarrow a=b=c=0\), loại

TH2: \(abc=1\). Ta dễ dàng suy ra được \(a+b+c=ab+bc+ca\). Ta có \(\left(a-1\right)\left(b-1\right)\left(c-1\right)\) \(=abc-\left(ab+bc+ca\right)+\left(a+b+c\right)-1\) \(=0\) nên suy ra \(\left[{}\begin{matrix}a=1\\b=1\\c=1\end{matrix}\right.\). Giả sử \(a=1\). Khi đó ta có \(bc=1\)

 Thay lại vào 2 pt đã cho, ta đều thấy thỏa mãn. Vậy ta tìm được 1 tập nghiệm của hệ là \(S_1=\left\{\left(a;b;c\right)|a=1;bc=1\right\}\) và các hoán vị của mỗi nghiệm thuộc tập S₁.

 TH3: \(abc=-1\). Ta kiểm chứng được \(a+b+c+ab+bc+ca=0\). Ta có \(\left(a+1\right)\left(b+1\right)\left(c+1\right)=abc+ab+bc+ca+a+b+c+1=0\) nên \(\left[{}\begin{matrix}a=-1\\b=-1\\c=-1\end{matrix}\right.\). Nếu \(a=-1\) thì suy ra \(bc=1\). Thử lại vào cả 2 pt ta đều thấy thỏa mãn. Như vậy ta tìm được tập nghiệm nữa của hpt đã cho là \(S_2=\left\{\left(a;b;c\right)|a=-1;bc=1\right\}\) và các hoán vị của mỗi bộ nghiệm trong các nghiệm thuộc \(S_2\).

 Vậy tập nghiệm của hpt đã cho là \(S=S_1\cup S_2=\left\{\left(a;b;c\right)|a=\pm1;bc=1\right\}\) và các hoán vị của mỗi phần tử thuộc S.

A = \(x^2\) - 4\(x\) + 2018

A = \(x^2\) - 4\(x\) + 4 + 2014

A= (\(x\) - 2)² + 2014

Vì (\(x\) - 2)² ≥ 0; ⇒ (\(x\) - 2)² + 2014 ≥ 2014

A(min) = 2014 ⇔ \(x\) -  2= 0 ⇔ \(x\) = 2

Kết luận giá trị nhỏ nhất của biểu thức A là 2014 xảy ra khi \(x\) = 2

B = 4\(x^2\) + 12\(x\) + 20 

B = (4\(x^2\) + 12\(x\) + 9) + 11

B = 4.(\(x^2\) + 3\(x\) + \(\dfrac{9}{4}\)) + 11

B =4.(\(x^2\) + 2.\(\dfrac{3}{2}\)\(x\) + \(\left(\dfrac{3}{2}\right)^2\)) + 11

B = 4.(\(x\) + \(\dfrac{3}{2}\))² + 11

Vì (\(x\) + \(\dfrac{3}{2}\))² ≥ 0 ⇒ 4.(\(x\) + \(\dfrac{3}{2}\))²  + 11 ≥ 11

Vậy B(min) = 11 ⇔ \(x\) + \(\dfrac{3}{2}\) = 0⇔ \(x\) = - \(\dfrac{3}{2}\) 

Kết luận giá trị nhỏ  nhất của biểu thức B là: 11 xảy ra khi \(x\) = - \(\dfrac{3}{2}\)

A = �2x2 - 4$x$ + 2018

A = �2x2 - 4$x$ + 4 + 2014

A= ($x$ - 2)2 + 2014

Vì ($x$ - 2)2 ≥ 0; ⇒ ($x$ - 2)2 + 2014 ≥ 2014

A(min) = 2014 ⇔ $x$ -  2= 0 ⇔ $x$ = 2

Kết luận giá trị nhỏ nhất của biểu thức A là 2014 xảy ra khi $x$ = 2

B = 4�2x2 + 12$x$ + 20 

B = (4�2x2 + 12$x$ + 9) + 11

B = 4.(�2x2 + 3$x$ + 9449​) + 11

B =4.(�2x2 + 2.3223​$x$ + (32)2(23​)2) + 11

B = 4.($x$ + 3223​)2 + 11

Vì ($x$ + 3223​)2 ≥ 0 ⇒ 4.($x$ + 3223​)2  + 11 ≥ 11

Vậy B(min) = 11 ⇔ $x$ + 3223​ = 0⇔ $x$ = - 3223​ 

Kết luận giá trị nhỏ  nhất của biểu thức B là: 11 xảy ra khi $x$ = - 3223​
 

Ta có \(27=xy+yz+zx\ge3\sqrt[3]{\left(xyz\right)^2}\) \(\Leftrightarrow9\ge\sqrt[3]{\left(xyz\right)^2}\) \(\Leftrightarrow729\ge\left(xyz\right)^2\) \(\Leftrightarrow27\ge xyz\) \(\Leftrightarrow27\left(xyz\right)^2\ge\left(xyz\right)^3\) \(\Leftrightarrow\sqrt{3}\sqrt[3]{xyz}\ge\sqrt{xyz}\) (lấy căn bậc 6 2 vế) \(\Leftrightarrow3\sqrt[3]{xyz}\ge\sqrt{3xyz}\)

Do đó \(x+y+z\ge3\sqrt[3]{xyz}\ge\sqrt{3xyz}\). ĐTXR \(\Leftrightarrow x=y=z=3\) 

Tham khảo nhé 

Khi ta nhai cơm lâu trong miệng thấy có cảm giác ngọt vì tinh bột trong cơm đã chịu tác dụng của enzim amilaza trong nước bọt và biến đổi một thành phần thành đường mantôzơ, đường này đã tác động vào các gai vị giác trên lưỡi cho ta cảm giác ngọt.

\(\dfrac{1}{8}\) + \(\dfrac{5}{7}\) = \(\dfrac{7}{56}\) + \(\dfrac{40}{56}\) = \(\dfrac{47}{56}\)

81​ + 5775​ = 756567​ + 40565640​ = 47565647​

 

7 \(\times\) ( 2\(x\) - 5) - 5 \(\times\) (7\(x\) - 2) + 2 \(\times\) (5\(x\) - 7) = (\(x\) - 2) - (\(x\) +4)

14\(x\) - 35 - 35\(x\) + 10 + 10\(x\) - 14 = \(x\) - 2 - \(x\) - 4

(14\(x\) - 35\(x\) + 10\(x\)) - (35 - 10+ 14)  = -6

(- 21 \(x\) + 10\(x\)) - (25 + 14) = - 6

         -11\(x\) - 39 = - 6

          -11\(x\)       = - 6 + 39

          - 11\(x\)     = 33

                \(x\) = 33 : (-11)

                \(x\) =  - 3

14x - 35 -35x + 10 + 10x - 14 = x-2-x-4

-11x -39 = -6

11x = -33

x= -3