tìm điều kiện n-2 là ước của 3n+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) -4/5 = -28/35
6/7 = 30/35
b) -2/21 = -16/168
5/(-24) = -35/168
c) -7/12 = -21/36
11/(-18) = -22/36
d) -15/45 = -1/3 = -5/15
-12/60 = -1/5 = -3/15
e) 3/20 = 9/60
4/30 = 8/60
7/15 = 28/60
f) -5/16 = -105/334
11/24 = 154/334
-21/56 = -126/334

Dùng Cách phối hợp nhiều phương pháp em nhé!
Đó là phương pháp chặn kết hợp với tìm nghiệm nguyên.
Gọi số đó là A thì theo bài ra ta có:
A = 2023.k + 228 (k \(\in\) N* )
A = 2024n + 218 (n \(\in\) N*)
⇒ 2023k + 228 = 2024n + 218
⇒ 2024n + 218 - 228 = 2023k
⇒ 2024n - 10 = 2023k
⇒ k = \(\dfrac{2024n-10}{2023}\)
⇒ k = n + \(\dfrac{n-10}{2023}\)
vì k nguyên nên n - 10 ⋮ 2023
⇒n - 10 \(\in\) B(2023) = {0; 2023;...;}
⇒ n \(\in\) {10; 2033;..;} (1)
Vì A là số có 5 chữ số nên A ≤ 99999
⇒ 2024n + 218 ≤ 99999
2024n ≤ 99999 - 218
2024n ≤ 99781
n ≤ 99781 : 2024
n ≤ 49,298 (2)
Kết hợp 1 và (2) ta có: n = 10
Vậy số cần tìm là: 2024 x 10 + 218 = 20458
Kết luận:...

** Bổ sung thêm điều kiện $x,y$ là số nguyên.
Lời giải:
Với $x,y$ nguyên thì $x-2, x-y+5$ cũng là số nguyên. Mà $(x-2)(x-y+5)=11$ nên ta có các TH sau:
TH1:
$x-2=1, x-y+5=11\Rightarrow x=3; y=-3$ (thỏa mãn)
TH2:
$x-2=-1, x-y+5=-11\Rightarrow x=1; y=17$ (thỏa mãn)
TH3:
$x-2=11, x-y+5=1\Rightarrow x=13; y=17$ (thỏa mãn)
TH4:
$x-2=-11; x-y+5=-1\Rightarrow x=-9; y=-3$ (thỏa mãn)

Lời giải:
$12A=1.5.12+5.9.(13-1)+9.13(17-5)+13.17(21-9)+....+77.81(85-73)+81.85(89-77)$
$=60+(5.9.13+9.13.17+13.17.21+...+77.81.85+81.85.89)-(1.5.9+5.9.13+9.13.17+...+73.77.81+77.81.85)$
$=60+81.85.89 - 1.5.9=612780$
A = 1.5 + 5.9 + 9.13 + ... + 81.85
A = \(\dfrac{12}{12}\)(1.5 + 5.9 + 9.13 + 81.85)
A = \(\dfrac{1}{12}\).(1.5.12 + 5.9.12.+ 9.13.12 + ...+ 81.85.12]
A = \(\dfrac{1}{12}\).[1.5.(9 + 3) + 5.9.(13 - 1) + 9.13.(17 - 5) +...+ 81.85.(89 - 77)]
A = \(\dfrac{1}{12}\).[1.5.9 + 1.3.5 + 5.9.13 - 5.9.1 + 9.13.17 - 9.13.5 + ...+ 81.85.89 - 81.85.77]
A = \(\dfrac{1}{12}\).[1.3.5 + 81.85.89]
A = \(\dfrac{1}{12}\).[15 + 612765]
A = \(\dfrac{1}{12}\).612780
A = 51065


Bạn cần hỗ trợ bài nào bạn nên ghi chú rõ bài đó ra nhé.
Bài 1:
a; Các số nguyên đã cho được sắp xếp theo thứ tự tăng dần là:
-2024; - 199; -99; -1; 10; 12; 2023
b; Các số nguyên thỏa mãn đề bài là:
-7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5
Tổng các số nguyên thỏa mãn đề bài là:
-7 + (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5
= - (7 + 6) + [(-5) + 5] + [(-4)+ 4] + [(-3) + 3]+ [(-2) + 2]+[(-1) + 1] + 0
= -13 + 0 + 0 +...+ 0
= - 13

Ta có \(a^n-a^{n-4}=a^{n-4}\left(a^4-1\right)=N\)
Ta thấy vì \(a^{n-4}\) và \(a^4-1\) không cùng tính chẵn lẻ nên \(N⋮2\)
Mặt khác, ta thấy nếu \(a⋮3\) thì hiển nhiên \(N⋮3\). Nếu \(a⋮̸3\) thì \(a^2\) chia 3 dư 1 (tính chất số chính phương), dẫn tới \(a^4=\left(a^2\right)^2\) chỉ có thể chia 3 dư 1 hay \(a^4-1⋮3\) với mọi \(a⋮̸3\). Vậy \(N⋮3\)
Ta cần chứng minh \(N⋮5\).
Dễ thấy điều này đúng nếu \(a⋮5\)
Với \(a⋮̸5\), khi đó \(a^2\) chia 5 dư 1 hoặc 4 (tính chất của số chính phương), suy ra \(a^4=\left(a^2\right)^2\) chia 5 chỉ có thể dư 1 (cũng là tính chất của số chính phương). Dẫn đến \(a^4-1⋮5\) với mọi \(a⋮̸5\). Vậy \(N⋮5\).
Do đó \(N⋮2.3.5=30\) (đpcm)
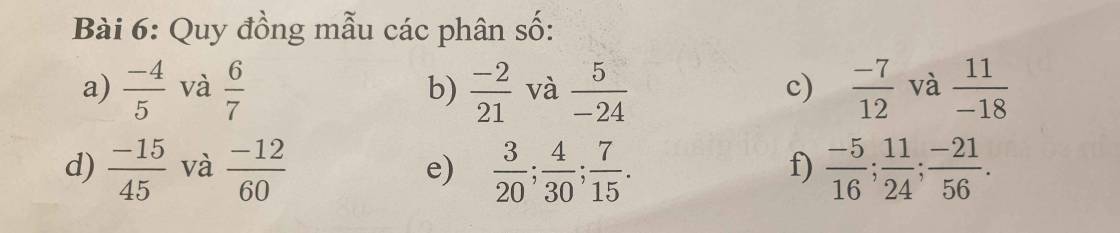
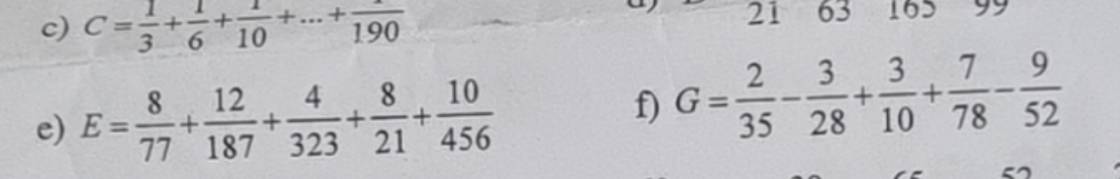

giúp với