Tích 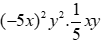
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`@` `\text {Ans}`
`\downarrow`
\(3(x^2+2x-3)+3(-x^2-4x)\)
`= 3*(x^2+2x-3 - x^2 - 4x)`
`= 3*[(x^2-x^2)+(2x-4x)-3]`
`= 3*(-2x-3)`
`= -6x-9`
3(x² + 2x - 3) + 3(-x² - 4x)
= 3x² + 6x - 9 - 3x² - 12x
= (3x² - 3x²) + (6x - 12x) - 9
= -6x - 9

Với x, y là hai số dương, dễ dàng chứng minh x + y 2,
do x + y = 2 => 0 < xy ≤ 1 (1)
Ta lại có: 2xy( x2 + y2) ≤
=> 0 < 2xy(x2 + y2) ≤ (x+y)4/4 = 4
=> 0 < xy( x2 + y2) ≤ 2 (2)
Nhân (1) với (2) theo vế ta có: x2y2 ( x2 + y2) ≤ 2 (đpcm)
Dấu “=” xảy ra khi x = y = 1

1. B (nếu gạch chữ "a")
2. C (nếu gạch chữ "e")
3. D (nếu gạch chữ "u")
4. D (nếu gạch "ou")
5. C (nếu gạch chữ "c")

1. A. flat B. hat C. casual D. equal
2. A. question B. location C. nation D. animation
3. A. design B. side C. picnic D. advice
4. A. gum B. hunt C. tunnel D. tunic
5. A. learned B. dressed C. guided D. wanted
6. A. origami B. prize C. divide D. like
7. A. comedy B. leisure C. cinema D. celebration
8. A. adore B. fancy C. attract D. alive
9. A. bread B. read C. meat D. peach
10. A. school B. church C. children D. watch
11. A. sound B. out C. found D. enough
12. A. bracelet B. favourite C. craft D. game
13. A. leisure B. sure C. shopping D. socialise
14. A. trick B. kit C. addict D. virtual
15. A. satisfied B. hooked C. bored D. socialised
16. A. sound B. cloud C. found D. favorite
17. A. tool B. noon C. door ` D. school
18. A. know B. show C. now D. low
19. A. crafts B. teenagers C. streets D. stamps
20. A. mention B. suggestion C. action D. education
21. A. leisure B. eight C. celebrate D. penalty
22. A. fun B. sun C. surf D. cut
23. A. bracelet B. cake C. make D. hat
24. A. although B. laugh C. paragraph D. enough
25. A. comedy B. novel C. princess D. cinema
26. A. addicted B. virtual C. kit D. active
27. A. communicate B. produce C. computer D. summer
28. A. pressure B. especial C. prepare D. helpful
29. A. hooked B. book C. school D. foot
30. A. wanted B. booked C. hooked D. stopped
\(Errink\times Cream\)

Câu 1:
Ta thấy \(S_2=\dfrac{\sqrt{3}+S_1}{1-\sqrt{3}S_1}=\dfrac{\sqrt{3}+1}{1-\sqrt{3}}=\dfrac{\left(1+\sqrt{3}\right)^2}{\left(1-\sqrt{3}\right)\left(1+\sqrt{3}\right)}\)\(=\dfrac{4+2\sqrt{3}}{-2}=-2-\sqrt{3}\)
Từ đó \(S_3=\dfrac{\sqrt{3}+S_2}{1-\sqrt{3}S_2}=\dfrac{\sqrt{3}-2-\sqrt{3}}{1-\sqrt{3}\left(-2-\sqrt{3}\right)}=\dfrac{-2}{4+2\sqrt{3}}=\dfrac{1}{-2-\sqrt{3}}\)
và \(S_4=\dfrac{\sqrt{3}+S_3}{1-\sqrt{3}S_3}=\dfrac{\sqrt{3}+\dfrac{1}{-2-\sqrt{3}}}{1-\dfrac{\sqrt{3}}{-2-\sqrt{3}}}=\dfrac{-2\sqrt{3}-3+1}{-2-\sqrt{3}-\sqrt{3}}=1\)
Đến đây ta thấy \(S_4=S_1\). Cứ tiếp tục làm như trên, ta rút ra được:
\(S_{3k+1}=1\); \(S_{3k+2}=-2-\sqrt{3}\) và \(S_{3k+3}=\dfrac{1}{-2-\sqrt{3}}\), với \(k\inℕ\)
Ta tính số các số thuộc mỗi dạng \(S_{3k+i}\left(i=1,2,3\right)\) từ \(S_1\) đến \(S_{2017}\).
- Số các số hạng có dạng \(S_{3k+1}\) là \(\left(2017-1\right):3+1=673\) số
- Số các số hạng có dạng \(S_{3k+2}\) là \(\left(2015-2\right):3+1=672\) số
- Số các số hạng có dạng \(S_{3k+3}\) là \(\left(2016-3\right):3+1=672\) số
Như thế, tổng S có thể được viết lại thành
\(S=\left(S_1+S_4+...+S_{2017}\right)+\left(S_2+S_5+...+S_{2015}\right)+\left(S_3+S_6+...+S_{2016}\right)\)
\(S=613+612\left(-2-\sqrt{3}\right)+612\left(\dfrac{1}{-2-\sqrt{3}}\right)\)
Tới đây mình lười rút gọn lắm, nhưng ý tưởng làm bài này là như vậy.
Có \(\left(x-\sqrt{x^2+5}\right).\left(y-\sqrt{y^2+5}\right)=5\) (1)
\(\Leftrightarrow\dfrac{\left(x-\sqrt{x^2+5}\right).\left(x+\sqrt{x^2+5}\right)}{x+\sqrt{x^2+5}}.\dfrac{\left(y-\sqrt{y^2+5}\right).\left(y+\sqrt{y^2+5}\right)}{y+\sqrt{y^2+5}}=5\)
\(\Leftrightarrow\left(x+\sqrt{x^2+5}\right).\left(y+\sqrt{y^2+5}\right)=5\) (2)
Từ (1) và (2) ta có \(\left(x-\sqrt{x^2+5}\right).\left(y-\sqrt{y^2+5}\right)=\left(x+\sqrt{x^2+5}\right).\left(y+\sqrt{y^2+5}\right)\)
\(\Leftrightarrow x\sqrt{y^2+5}+y\sqrt{x^2+5}=0\)
\(\Leftrightarrow x^2\left(y^2+5\right)=y^2\left(x^2+5\right)\left(y\le0;x\ge0\right)\)
\(\Leftrightarrow x^2-y^2=0\Leftrightarrow\left[{}\begin{matrix}x=y\left(\text{loại}\right)\\x=-y\left(\text{nhận}\right)\end{matrix}\right.\)
Khi đó M = x3 + y3 = 0
N = x2 + y2 = 2y2


Ta biến đổi \(A=\dfrac{2-1}{1.2}+\dfrac{4-3}{3.4}+...+\dfrac{2016-2015}{2016.2015}+\dfrac{2018-2017}{2017.2018}\)
\(A=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2015}-\dfrac{1}{2016}+\dfrac{1}{2017}-\dfrac{1}{2018}\)
\(A=\left(1+\dfrac{1}{3}+...+\dfrac{1}{2017}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)
\(A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2017}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)
\(A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2017}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{1009}\right)\)
\(A=\dfrac{1}{1010}+\dfrac{1}{1011}+...+\dfrac{1}{2017}+\dfrac{1}{2018}\)
Lại có \(B=\dfrac{1}{1010.2018}+\dfrac{1}{1011.2017}+...+\dfrac{1}{2018.1010}\)
\(B=\dfrac{1}{3028}.\left(\dfrac{3028}{1010.2018}+\dfrac{3028}{1011.2017}+...+\dfrac{3028}{2018.1010}\right)\)
\(B=\dfrac{1}{3028}\left(\dfrac{1}{1010}+\dfrac{1}{2018}+\dfrac{1}{1011}+\dfrac{1}{2017}+...+\dfrac{1}{2018}+\dfrac{1}{1010}\right)\)
\(B=\dfrac{1}{3028}.2\left(\dfrac{1}{1010}+\dfrac{1}{1011}+...+\dfrac{1}{2018}\right)\)
\(B=\dfrac{1}{3028}.2A\) \(\Rightarrow\dfrac{A}{B}=1514\inℤ\). Ta có đpcm

Sửa: `+12y^2 -> -12y^2`
\(7x^2-5xy-12y^2\\ =7x^2+7xy-12xy-12y^2\\ =7x\left(x+y\right)-12y\left(x+y\right)\\ =\left(7x-12y\right)\left(x+y\right)\)
\(\left(-5x^2\right)y^2.\dfrac{1}{5}xy\)
\(=\left(-5x^2y^2\right).\dfrac{1}{5}xy\)
\(=-x^3y^3\)