ƯCLN ( 735, 441, 294 ) =
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Điều kiện: $x\neq 0$
Với $x\neq 0$ thì khi $x\vdots 6\Rightarrow |x|\geq |6|$
Hay $|x|\geq 6(1)$
$6\vdots x\Rightarrow |6|\geq |x|$ hay $6\geq |x|(2)$
Từ $(1); (2)\Rightarrow |x|=6\Leftrightarrow x=\pm 6$

Ta có: `gcd(450;60)=30` nên độ dài viên gạch lớn nhất có thể là `30cm`

- Mười nghìn và một triệu: KHÔNG LÀ HAI SỐ NGUYÊN TỐ CÙNG NHAU. Vì nó cùng chia hết cho 2.
- Hai số tự nhiên liên tiếp: LÀ HAI SỐ NGUYÊN TỐ CÙNG NHAU.
Gọi `d=(2a-1,2a+1)(d,a\inNN^(**);\text(d lẻ ))=>(2a+1)-(2a-1)\vdots d=>2\vdots d =>d\in{1;2}=>d=1`( do `d` lẻ `)`
- `2n+3` và `3n+4` với `n\in N^(**):` LÀ HAI SỐ NGUYÊN TỐ CÙNG NHAU.
Gọi `d=(2n+3;3n+4)=d(d\inNN^(**); \text(d lẻ))=>3(2n+3)-2(3n+4)\vdots d <=>1\vdots d =>d=1`

3 tấn= 3000 kg
Số bao thóc bác dùng chứa thóc:
3000: 89= 33 (bao) (dư 63kg)
63kg thóc dư được cho vào 1 bao khác
Vậy bác nông dân cần chuẩn bị ít nhất 34 bao để chứa hết 3 tấn thóc

\(40=2^3.5\\ 52=2^2.13\\ BCNN\left(40;52\right)=2^3.5.13=520\\ MSC=B\left(520\right)=\left\{0;520;1040;1560;2080;2600;...\right\}\\ Chọn:520\)

a, Ngày Hạ chí năm 2023 là thứ tư
b, Ngày Hạ chí năm 2032 (sau 10 năm với 3 năm nhuận là 2024, 2028, 2032 và 7 năm không nhuận), mỗi năm nhuận là 52 tuần và lẻ 2 ngày, mỗi năm không nhuận là 52 tuần và lẻ 1 ngày. Tổng số ngày lẻ trong 10 năm đó: 2 x 3 + 7 x 1 = 13 (ngày) < 14 (ngày)
Vậy ngày Hạ chí năm 2032 là vào thứ hai

\(S=3+3^2+3^3+3^4+3^5+3^6+3^7+3^8+3^9\\ =\left(3+3^2+3^3\right)+3^3.\left(3+3^2+3^3\right)+3^6.\left(3+3^2+3^3\right)\\ =39+3^3.39+3^6.39\\ =-39.\left(-1-3^3-3^6\right)⋮\left(-39\right)\)
S = 3 + 32 + 33 + 34 + 35 + 36 + 37 + 38 + 39
S = ( 3 + 32 + 33 ) +34 + 35 + 36 + 37 + 38 + 39
S = 39 + 34 + 35 + 36 + 37 + 38 + 39
Vì 39 ⋮ -39
<=> S ⋮ -39

a, \(\overline{20x5}\) \(⋮\) 9 ⇔ 2 + 0 + 5 + \(x\) ⋮ 9 ⇔ \(x\) + 2 ⋮ 9 ⇒ \(x\) = 7
Vậy \(x=7\)
b, \(\overline{x998y}\) \(⋮\) 2; 3 và 5
\(\overline{x998y}\) \(⋮\) 2 và 5 ⇔ \(y\) = 0
\(\overline{x998y}\) \(⋮\) 3 ⇔ \(x+9+9+8\) +y ⋮ 3 ⇒ \(x\) + 2 ⋮ 3 ⇒ \(x\) = 1; 4; 7
Vậy các cặp \(x;y\) thỏa mãn đề bài lần lượt là:
(\(x;y\)) =(1; 0); (4; 0); (7; 0)
c, \(\overline{87xy}\) \(⋮\) 9 ⇔ 8 + 7 + \(x+y\) ⋮ 9 ⇒ \(x+y\) + 6 ⋮ 9
\(x-y=4\) ⇒ \(x=4+y\). Thay \(x\) = 4 + y vào biểu thức \(x+y+6\)⋮9
ta có: 4+\(y+y\) +6 \(⋮\) 9 ⇒ 1 + 2⋮ 9 ⇒ 2\(y\) = 8⇒ y =4; \(x\) = 4+4 =8
Vậy \(x=8;y=4\)

a, Ư(7) = { -7; -1; 1; 7}
Lập bảng ta có:
| a +2 | -7 | -1 | 1 | 7 |
| a | -9 | -3 | -1 | 5 |
Theo bảng trên ta có:
\(a\) \(\in\) { -9; -3; -1; 5}
b, 2a + 1 \(\in\) Ư(12)
Ư(12) = { -12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}
lập bảng ta có:
| 2a+1 | -12 | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | 12 |
|
a
|
-11/2 loại |
-7/2 loại |
-5/2 loại |
-2 nhận |
-3/2 loại |
-1 nhận |
0 nhận |
1/2 loại |
1 nhận |
3/2 loại |
5/2 loại |
11/2 loại |
Theo bảng trên ta có các giá trị nguyên của a thỏa mãn đề bài là:
a \(\in\) {- 2; - 1; 0; 1}
n + 5 \(⋮\) n - 2
n - 2 + 7 ⋮ n - 2
7 ⋮ n -2
Ư(7) ={ -7; -1; 1; 7}
Lập bảng ta có:
| n - 2 | -7 | -1 | 1 | 7 |
| n | -5 | 1 | 3 | 9 |
Theo bảng trên ta có:
n \(\in\) { -5; 1; 3; 9}

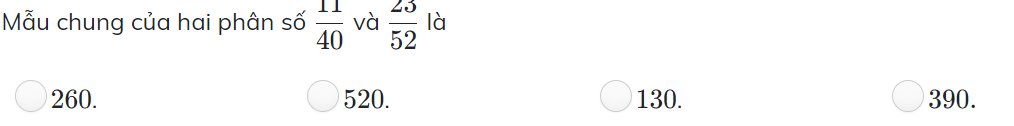
Ta có:
\(735=3\cdot5\cdot7^2\)
\(441=3^2\cdot7^2\)
\(294=2\cdot3\cdot7^2\)
\(\RightarrowƯCLN=\left(735,441,294\right)=3\cdot7^2=147\)
Bạn đăng sang môn toán nhé