\(\dfrac{1}{R\left(x\right)}=\dfrac{1}{x\left(x+2\right)}=\dfrac{1}{2}\left(\dfrac{1}{x}-\dfrac{1}{x+2}\right)\)

\(\Rightarrow S=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2022}-\dfrac{1}{2024}+\dfrac{1}{2023}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)

\(=\dfrac{1}{2}\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{2024}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)

Một kết quả rất xấu

108 độ

@Lê Thanh Sơn

Bạn phải giải chi tiết ra thì bạn Thu Thủy mới hiểu đc chứ đâu phải vèo cái đáp số lun đc!

ta có:

A là góc vuông nên A=90 độ

Ta lại có:

A+B+C=180 độ(tổng 3 góc trong 1 △)

90 độ+B+30 độ=180 độ

B=180-90-30

B=60 độ

Vì 90+60+30=180 độ

Nên C= 30 độ

mình không biết đánh dấu góc và độ bạn thông cảm bổ sung nhé

Nói thêm là mik cũng đang cố gắng để đc làm CTV nè!

mình cũng ko hiểu CTVVIP là gì

Lời giải:
a. Xét tam giác $ABM$ và $AHM$ có:

$AB=AH$

$AM$ chung

$\widehat{BAM}=\widehat{HAM}$ (do $AM$ là phân giác $\widehat{BAC}$)

$\Rightarrow \triangle ABM=\triangle AHM$ (c.g.c)

$\Rightarrow BM=HM$

b.

Gọi $O$ là giao điểm $AM, BH$

Xét tam giác $ABO$ và $AHO$ có:

$AB=AH$

$AO$ chung

$\widehat{BAO}=\widehat{HAO}$ (do $AM$ là phân giác $\widehat{BAC}$)

$\Rightarrow \triangle ABO=\triangle AHO$ (c.g.c)

$\Rightarrow \widehat{AOB}=\widehat{AOH}$

Mà $\widehat{AOB}+\widehat{AOH}=180^0$

$\Rightarrow \widehat{AOB}=\widehat{AOH}=90^0$

$\Rightarrow AM\perp BH$ tại $O$

c.

Từ tam giác bằng nhau phần a suy ra $BM=MH(1)$ và $\widehat{MHA}=\widehat{MBA}=90^0$

$\Rightarrow MH\perp AC$

$\Rightarrow MHC$ là tam giác vuông tại $H$

$\Rightarrow MC> MH$ (do $MC$ là cạnh huyền) (2)

Từ $(1); (2)\Rightarrow MC> MB$

Hình vẽ:

7a:40

7b:45

 Bởi : 1. Bạch Đằng Giang nằm cách cửa lục của vịnh Hạ Long 40km , nằm trong hệ thống sông Thái Bình . Đây được xem là con đường thủy chủ chốt để đi vào Hà Nội ; Đi từ cửa sông Trung Quốc thông qua sông Nam Triệu , qua sông Thầy , sông Đuống và qua sông Hồng Thăng Long 

-> Đây là đường tắt , nhiều đường ngặt nghèo : do có mật độ nước cao dễ diễn ra sóng lớn

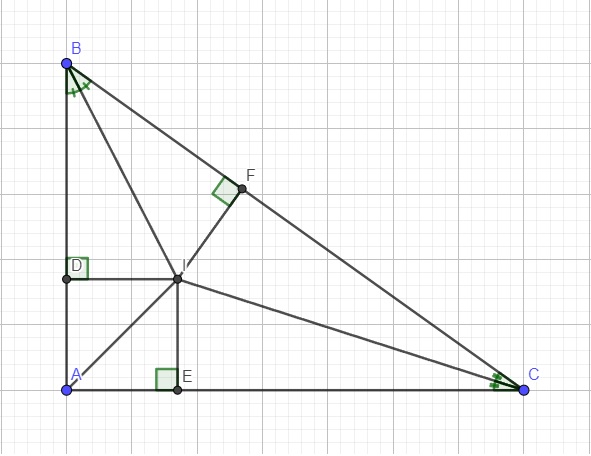
Do I là giao điểm 2 đường phân giác góc B và C nên AI cũng là phân giác góc A

ID vuông góc AB nên tam giác BID vuông tại D

IF vuông góc AC nên tam giác BIF vuông tại F

Xét hai tam giác vuông BID và BIF có:

\(\left\{{}\begin{matrix}BI\text{ là cạnh chung}\\\widehat{IBD}=\widehat{IBF}\left(\text{do IB là phân giác}\right)\end{matrix}\right.\) 

\(\Rightarrow\Delta_VBID=\Delta_VBIF\left(ch-gn\right)\)

\(\Rightarrow BD=BF\)

Chứng minh tương tự, ta cũng có: \(AD=AE\) ; \(CE=CF\)

Từ đó ta có:

\(\left(BA+BC-AC\right):2=\left(BD+AD+BF+CF-AE-CE\right):2\)

\(=\left(BD+BF\right):2=2BD:2=BD\) (đpcm)