
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
\(\Leftrightarrow\dfrac{x+4}{2000}+1+\dfrac{x+3}{2001}+1=\dfrac{x+2}{2002}+1+\dfrac{x+1}{2003}+1\)
\(\Leftrightarrow\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}=\dfrac{x+2004}{2002}+\dfrac{x+2004}{2003}\)
\(\Leftrightarrow\left(x+2004\right)\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)=0\Leftrightarrow x=-2004\)
\(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
=>\(\left(\dfrac{x+4}{2000}+1\right)+\left(\dfrac{x+3}{2001}+1\right)=\left(\dfrac{x+2}{2002}+1\right)+\left(\dfrac{x+1}{2003}+1\right)\)
=>\(\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}=\dfrac{x+2004}{2002}+\dfrac{x+2004}{2003}\)
=>\(\left(x+2004\right)\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)=0\)
=>x+2004=0
=>x=-2004

b, \(275-5\left(2x-1\right)=200\Leftrightarrow5\left(2x-1\right)=75\Leftrightarrow2x-1=15\Leftrightarrow x=8\)
c, \(3x-38:2=206\Leftrightarrow3x-19=206\Leftrightarrow3x=225\Leftrightarrow x=75\)
d, \(2x+x+5x=400\Leftrightarrow8x=400\Leftrightarrow x=50\)

\(sin^210+sin^220+sin^245+sin^270+sin^280\)
\(=sin^210+sin^220+sin^245+cos^220+cos^210=1+1+sin^245=2+\dfrac{1}{2}=\dfrac{5}{2}\)

(x-15):12=79 dư 8
=>\(x-15=79\times12+8=956\)
=>x=956+15=971
(x - 15) : 12 = 79 dư 8
x - 15 = 79 x 12 + 8
x - 15 = 956
x = 956 + 15
x= 971

\(\left\{47-\left[736:\left(5-3\right)^4\right]\right\}.2021\)
\(=\left\{47-\left[736:2^4\right]\right\}.2021\)
\(=\left\{47-\left[736:16\right]\right\}.2021\)
\(=\left\{47-46\right\}.2021\)
\(=1.2021\)
\(=2021\)
\(\left\{47-\left[736:\left(5-3\right)^4\right]\right\}\cdot2021\)
\(=\left\{47-736:16\right\}\cdot2021\)
\(=\left(47-46\right)\cdot2021=2021\)

2(x-1)+3(x-2)=x-4
=> 2x-2+3x-6=x-4
=> 5x-8=x-4
=> 5x-x=8-4
=> 4x=4
=> x=4:4
=> x=1
Vậy: x=1
\(2\left(x-1\right)+3\left(x-2\right)=x-4\)
\(2x-2+3x-6=x-4\)
\(\left(2x+3x\right)-\left(2+6\right)=x-4\)
\(5x-8=x-4\)
\(5x-x=-4+8\)
\(4x=4\)
\(x=1\)


\(\left(7+x\right)-\left(21-13\right)=32\)
\(\left(7+x\right)-8=32\)
\(7+x=32+8\)
\(7+x=40\)
\(x=40-7\)
\(x=33\)
Vậy \(x=33\)
\(\left(7+x\right)-\left(21-13\right)=32\)
\(7+x-21+13=32\)
\(x+\left(7+13-21\right)=32\)
\(x-1=32\)
\(x=33\)
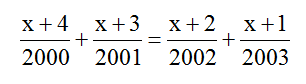


a: x+(x+1)+(x+2)+...+(x+30)=496
=>(x+x+...+x)+(1+2+3+...+30)=496
=>\(31x+30\times\dfrac{31}{2}=496\)
=>\(31x+465=496\)
=>31x=31
=>x=1
b: \(x+\left(x-1\right)+\left(x-2\right)+...+\left(x-50\right)=1530\)
=>\(51x-\left(1+2+3+...+50\right)=1530\)
=>\(51x-\dfrac{50\times51}{2}=1530\)
=>\(51x-1275=1530\)
=>51x=1275+1530=2805
=>x=2805:51=55
a, \(x+\left(x+1\right)+\left(x+2\right)+...+\left(x+30\right)=496\)
\(\Leftrightarrow31x+1+2+...+30=496\Leftrightarrow31x+\dfrac{\left(30+1\right).30}{2}=496\)
\(\Leftrightarrow31x+465=496\Leftrightarrow31x=31\Leftrightarrow x=1\)
b, \(x+\left(x-1\right)+\left(x-2\right)+...+\left(x-50\right)=1530\)
\(\Leftrightarrow51x+\dfrac{\left(-1-50\right).50}{2}=1530\Leftrightarrow51x-1275=1530\Leftrightarrow51x=2805\Leftrightarrow x=55\)