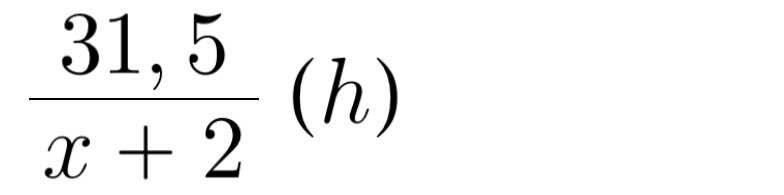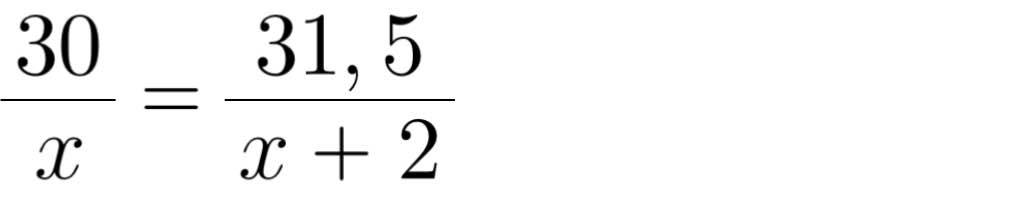Cho các số phức: z, w, u thay đổi thỏa mãn: \(\left|z\right|=\left|w\right|=5\) và: \(\left|z-w\right|^2=8\left|2u-z+w\right|\). Biết: \(\left(z-4i\right)\left(\overline{w}-4i\right)\) và: \(\left(2u+z-w-8i\right)\overline{\left(z-w-2u\right)}\) là các số thực dương. Giá trị nhỏ nhất của: \(P=\left|u-2+i\right|+\left|2u-1+3i\right|\) bằng:
A. \(3+\sqrt{2}\) B. \(\sqrt{34}\) C. \(\sqrt{26}\) D. \(3\sqrt{2}+1\)