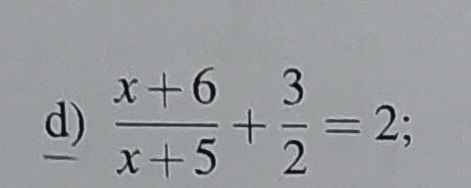 giải phương trình
giải phương trình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=\left(\dfrac{1}{2^2}-1\right)\cdot\left(\dfrac{1}{3^2}-1\right)\cdot...\cdot\left(\dfrac{1}{1000^2}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\cdot\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{1000}-1\right)\cdot\left(\dfrac{1}{2}+1\right)\cdot\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{1000}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-999}{1000}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot....\cdot\dfrac{1001}{1000}\)
\(=\dfrac{-1}{1000}\cdot\dfrac{1001}{2}=\dfrac{-1001}{2000}\)

\(B=2021\cdot2025=\left(2023-2\right)\cdot\left(2023+2\right)=2023^2-4=A-4\)
=>A lớn B 4 đơn vị

\(\left|x-3,5\right|=\dfrac{4}{7}\)
=>\(\left[{}\begin{matrix}x-\dfrac{7}{2}=\dfrac{4}{7}\\x-\dfrac{7}{2}=-\dfrac{4}{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{7}+\dfrac{7}{2}=\dfrac{8}{14}+\dfrac{49}{14}=\dfrac{57}{14}\\x=-\dfrac{4}{7}+\dfrac{7}{2}=\dfrac{-8}{14}+\dfrac{49}{18}=\dfrac{41}{14}\end{matrix}\right.\)

a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(DN=NC=\dfrac{DC}{2}\)
\(BE=EC=\dfrac{BC}{2}\)
mà AB=DC=BC
nên AM=MB=DN=NC=BE=EC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Xét ΔMBC vuông tại B và ΔECD vuông tại C có
MB=EC
BC=CD
Do đó: ΔMBC=ΔECD
=>\(\widehat{BMC}=\widehat{CED}\)
=>\(\widehat{CED}+\widehat{ECM}=90^0\)
=>CM\(\perp\)DE
c: ΔMBC=ΔECD
=>MC=ED

Bài 5:
a: \(A=23-21+19-17+15-13+11-9+7-5+3-1\)
=(23-21)+(19-17)+(15-13)+(11-9)+(7-5)+(3-1)
=2+2+2+2+2+2
=12
b: \(B=24-22+20-18+16-14+12-10+8-6+4-2\)
=(24-22)+(20-18)+(16-14)+(12-10)+(8-6)+(4-2)
=2+2+2+2+2+2
=12
c: \(C=3+5+7+9+11+13+15+17+19\)
=(3+19)+(5+17)+(7+15)+(9+13)+11
=22+22+22+22+11
=99
d: Số số hạng là \(\dfrac{101-3}{2}+1=\dfrac{98}{2}+1=50\left(số\right)\)
Tổng của dãy số là:
\(D=\left(101+3\right)\cdot\dfrac{50}{2}=104\cdot25=2600\)
Bài 4:
1: \(13\cdot58\cdot4+32\cdot26\cdot2+52\cdot10\)
\(=52\cdot58+52\cdot32+52\cdot10\)
\(=52\left(58+32+10\right)=52\cdot100=5200\)
2: \(15\cdot37\cdot4+120\cdot21+21\cdot5\cdot12\)
\(=60\cdot37+60\cdot42+60\cdot21\)
=60(37+42+21)
=60*100=6000
3: \(14\cdot35\cdot5+10\cdot25\cdot7+20\cdot70\)
\(=70\cdot35+70\cdot25+70\cdot20\)
\(=70\left(35+25+20\right)=70\cdot80=5600\)
4: \(15\cdot\left(27+18+6\right)+15\cdot\left(23+12\right)\)
\(=15\cdot\left(45+6+35\right)=15\cdot86=1290\)
5: \(24\cdot\left(15+49\right)+12\cdot\left(50+42\right)\)
\(=24\cdot64+12\cdot92=24\cdot64+24\cdot46=24\cdot\left(64+46\right)\)
\(=24\cdot110=2640\)

a: 11+13+15+17+19
=(11+19)+(13+17)+15
=30+30+15
=75
b: \(122+2116+278+84\)
=(122+278)+(2116+84)
=400+2200
=2600
c: \(12\times125\times54\)
=1500x54
=81000
d: \(27\times36+27\times64=27\times\left(36+64\right)=27\times100=2700\)
e: \(25\text{x}37+25\text{x}63-150\)
=25x(37+63)-150
=25x100-150
=2500-150
=2350
f: \(425\text{x}74-27\text{x}425-1\)
=425x(74-27-1)
=425x46=19550
g: \(8\text{x}9\text{x}14+6\text{x}17\text{x}12+19\text{x}4\text{x}18\)
=14x72+17x72+19x72
=72x(14+17+19)
=50x72=3600
a) $11+13+15+17+19$
$=(11+19)+(13+17)+15$
$=30+30+15$
$=60+15=75$
b) $122+2116+278+84$
$=(122+278)+(2116+84)$
$=400+2200=2600$
c) $12\times125\times54$
$=3\times4\times125\times2\times27$
$=(4\times2)\times125\times(3\times27)$
$=8\times125\times81$
$=1000\times81=81000$
d) $27\times36+27\times64$
$=27\times(36+64)$
$=27\times100=2700$
e) $25\times37+25\times63-150$
$=25\times(37+63)-150$
$=25\times100-150$
$=2500-150=2350$
f) $425\times74-27\times425-425$
$=425\times(74-27-1)$
$=425\times(47-1)$
$=425\times46=19550$
g) $8\times9\times14+6\times17\times12+19\times4\times18$
$=(8\times9)\times14+(6\times12)\times17+(4\times18)\times19$
$=72\times14+72\times17+72\times19$
$=72\times(14+17+19)$
$=72\times(31+19)$
$=72\times50=3600$
$\mathtt{Toru}$

Câu 1:
\(2\sin x-\sqrt{3}=0\\ \Leftrightarrow\sin x=\dfrac{\sqrt{3}}{2}=\sin\dfrac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{\pi}{3}+k_12\pi\\x_2=\pi-\dfrac{\pi}{3}+k_22\pi=\dfrac{2\pi}{3}+k_22\pi\end{matrix}\right.\left(k_1,k_2\inℤ\right)\)
Mà: \(x\in\left[0;2\pi\right]\) do đó nên: \(k_1=0,k_2=0\)
Vậy tập nghiệm pt là: \(S=\left\{\dfrac{\pi}{3};\dfrac{2\pi}{3}\right\}\) (2 nghiệm => D)
Câu 2:
Vì: \(-1\le\cos x\le1\forall x\)
\(\Rightarrow-1\le m+1\le1\\ \Leftrightarrow-2\le m\le0\)
Mà: \(m\inℤ\Rightarrow m\in\left\{-2;-1;0\right\}\) (C)
Câu 1: \(2\cdot sinx-\sqrt{3}=0\)
=>\(sinx=\dfrac{\sqrt{3}}{2}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{3}+k2\Omega\\x=\Omega-\dfrac{\Omega}{3}+k2\Omega=\dfrac{2}{3}\Omega+k2\Omega\end{matrix}\right.\)
Để \(x\in\left[0;2\Omega\right]\) thì \(\left[{}\begin{matrix}\dfrac{\Omega}{3}+k2\Omega\in\left[0;2\Omega\right]\\\dfrac{2}{3}\Omega+k2\Omega\in\left[0;2\Omega\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2k+\dfrac{1}{3}\in\left[0;2\right]\\2k+\dfrac{2}{3}\in\left[0;2\right]\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2k\in\left[-\dfrac{1}{3};\dfrac{5}{3}\right]\\2k\in\left[-\dfrac{2}{3};\dfrac{4}{3}\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}k\in\left[-\dfrac{1}{6};\dfrac{5}{6}\right]\\k\in\left[-\dfrac{1}{3};\dfrac{2}{3}\right]\end{matrix}\right.\Leftrightarrow k=0\)
=>Chọn B
Câu 2:
Để phương trình cosx =m+1 có nghiệm thì -1<=m+1<=1
=>-2<=m<=0
mà m nguyên
nên \(m\in\left\{-2;-1;0\right\}\)
=>Chọn C

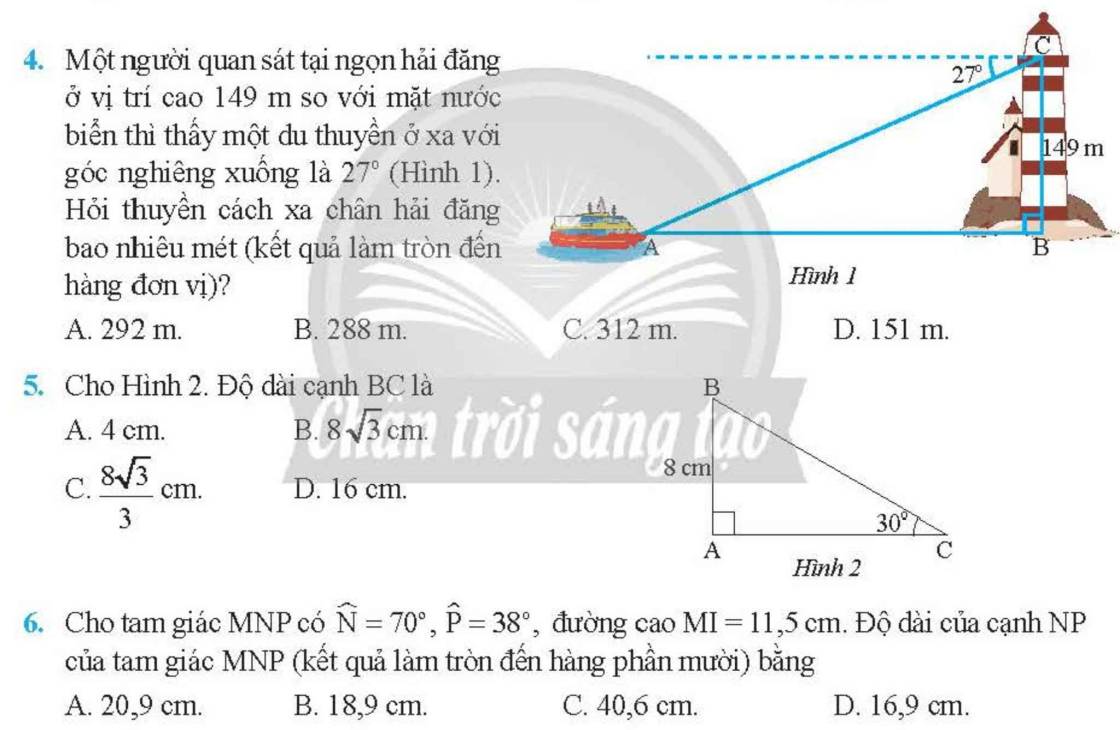
6:
Xét ΔMIN vuông tại I có \(tanN=\dfrac{MI}{NI}\)
=>\(NI=\dfrac{MI}{tanN}=\dfrac{11.5}{tan70}\simeq4,2\left(cm\right)\)
Xét ΔMIP vuông tại I có \(tanP=\dfrac{MI}{IP}\)
=>\(IP=\dfrac{MI}{tanP}=\dfrac{11.5}{tan38}\simeq14,7\left(cm\right)\)
NP=NI+IP=4,2+14,7=18,9(cm)
=>Chọn B
5: Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(BC=\dfrac{8}{sin30}=16\left(cm\right)\)
=>Chọn D
4:
\(\widehat{BAC}=27^0\)
Xét ΔBAC vuông tại B có \(tanBAC=\dfrac{BC}{BA}\)
=>\(BA=\dfrac{149}{tan27}\simeq292\left(m\right)\)
=>Chọn A

Bài 3:
a: \(3\in N;3\in Z;3\in Q\)
b: \(10\in N;10\in Z;10\in Q\)
c: \(-\dfrac{3}{7}\in Q\)
d: \(-2\in Z;-2\in Q\)
Bài 2:
\(\dfrac{-3}{5}=\dfrac{-27}{45};\dfrac{-5}{9}=\dfrac{-25}{45};-1\dfrac{2}{3}=\dfrac{-5}{3}=\dfrac{-75}{45};0,5=\dfrac{22,5}{45};\dfrac{10}{9}=\dfrac{50}{45}\)
mà -75<-27<-25<22,5<50
nên \(-1\dfrac{2}{3}< -\dfrac{3}{5}< -\dfrac{5}{9}< \dfrac{1}{2}< \dfrac{10}{9}\)
Bài 1:
a: \(\dfrac{9}{70}=\dfrac{9\cdot3}{70\cdot3}=\dfrac{27}{210};\dfrac{5}{42}=\dfrac{5\cdot5}{42\cdot5}=\dfrac{25}{210}\)
mà 27>25
nên \(\dfrac{9}{70}>\dfrac{5}{42}\)
b: \(\dfrac{-4}{27}=\dfrac{-4\cdot7}{27\cdot7}=\dfrac{-28}{189};\dfrac{10}{-63}=\dfrac{-10}{63}=\dfrac{-10\cdot3}{63\cdot3}=\dfrac{-30}{189}\)
mà -28>-30
nên \(\dfrac{-4}{27}>\dfrac{10}{-63}\)
c: \(\dfrac{999}{556}=1+\dfrac{443}{556};\dfrac{1000}{557}=1+\dfrac{443}{557}\)
mà \(\dfrac{443}{556}>\dfrac{443}{557}\)
nên \(\dfrac{999}{556}>\dfrac{1000}{557}\)
d: \(\dfrac{-2}{15}< 0;\dfrac{-10}{-11}=\dfrac{10}{11}>0\)
Do đó: \(\dfrac{-2}{15}< \dfrac{-10}{-11}\)
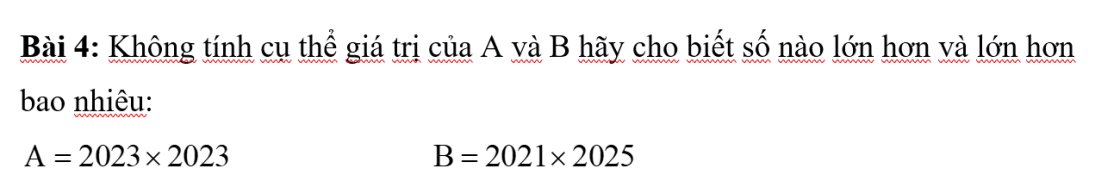

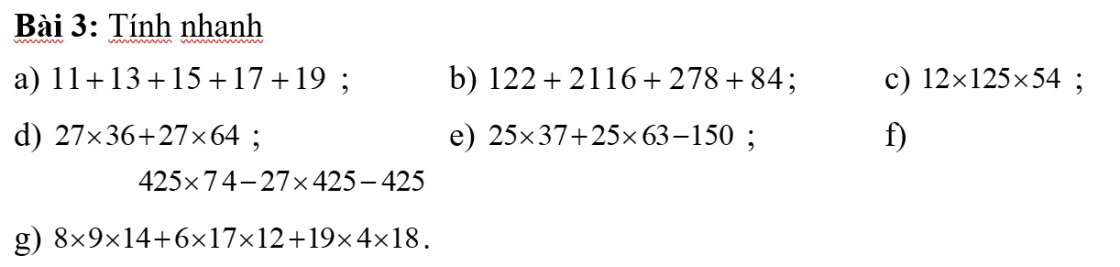
ĐKXĐ: \(x\ne-5\)
\(\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\)
\(\Leftrightarrow\dfrac{x+6}{x+5}=\dfrac{1}{2}\)
\(\Rightarrow2\left(x+6\right)=1.\left(x+5\right)\)
\(\Leftrightarrow2x+12=x+5\)
\(\Leftrightarrow2x-x=5-12\)
\(\Leftrightarrow x=-7\) (tm ĐKXĐ)
ĐKXĐ: \(x\ne-5\)
\(\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\)
=>\(\dfrac{x+6}{x+5}=2-\dfrac{3}{2}=\dfrac{1}{2}\)
=>\(2\left(x+6\right)=x+5\)
=>\(2x+12=x+5\)
=>2x-x=5-12
=>x=-7(nhận)