Nhân dịp nghỉ hè, bạn Hà được bố chở về quê thăm ông bà. Hai bố con xuất phát từ nhà lúc 5 giờ 40 phút, dự định đi với vận tốc không đổi là 30 km/giờ và có dừng lại 20 phút để nghỉ ngơi thì sẽ đến nơi lúc 10 giờ. Tuy nhiên, khi đi được 1 giờ thì xe bị hư, hai bố con phải dừng lại sửa xe mất 30 phút. Bố của Hà quyết định chạy xe không nghỉ với vận tốc tăng thêm 10 km/giờ so với dự định trên suốt quãng đường còn lại. Hỏi hai bố con đến nơi sớm hơn hay muộn hơn dự định ban đầu bao nhiêu phút
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: \(A=\left|-x+\dfrac{1}{7}\right|+\left|-x-\dfrac{3}{5}\right|-\dfrac{2}{6}\)
\(=\left|x-\dfrac{1}{7}\right|+\left|x+\dfrac{3}{5}\right|-\dfrac{1}{3}\)
\(-\dfrac{3}{5}< x< \dfrac{1}{7}\)
=>\(x+\dfrac{3}{5}>0;x-\dfrac{1}{7}< 0\)
=>\(A=\dfrac{1}{7}-x+x+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{1}{7}+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{43}{105}\)
d: \(A=\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+8\dfrac{1}{5}\)
\(=\left|x-2\dfrac{1}{5}\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)
\(\dfrac{1}{5}< =x< =2\dfrac{1}{5}\)
=>\(x-\dfrac{1}{5}>=0;x-2\dfrac{1}{5}< =0\)
=>\(D=2\dfrac{1}{5}-x+x-\dfrac{1}{5}+\dfrac{41}{5}=2+\dfrac{41}{5}=\dfrac{51}{5}\)

Vì AB//CD
nên ΔMAB~ΔMCD
=>\(\dfrac{S_{MAB}}{S_{MCD}}=\left(\dfrac{AB}{CD}\right)^2=\dfrac{1}{9}\)
=>\(\dfrac{S_{MAB}}{S_{ABCD}}=\dfrac{1}{8}\)
=>\(S_{MAB}=\dfrac{S_{ABCD}}{8}=3\left(cm^2\right)\)

\(B=\left(-\dfrac{1}{2}\right)+\left(-\dfrac{1}{6}\right)+\left(-\dfrac{1}{12}\right)+\left(-\dfrac{1}{20}\right)+\left(-\dfrac{1}{30}\right)+\left(-\dfrac{1}{42}\right)+\left(-\dfrac{1}{56}\right)+\left(-\dfrac{1}{72}\right)+\left(-\dfrac{1}{90}\right)\)
\(=-\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{90}\right)\)
\(=-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{9\cdot10}\right)\)
\(=-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=-\left(1-\dfrac{1}{10}\right)=-\dfrac{9}{10}\)

ĐKXĐ: x<>2
\(\dfrac{x-2}{8}=\dfrac{-2}{2-x}\cdot\dfrac{1}{3}\)
=>\(\dfrac{x-2}{8}=\dfrac{2}{x-2}\cdot\dfrac{1}{3}=\dfrac{2}{3\left(x-2\right)}\)
=>\(3\cdot\left(x-2\right)^2=16\)
=>\(\left(x-2\right)^2=\dfrac{16}{3}\)
=>\(\left[{}\begin{matrix}x-2=\dfrac{4}{\sqrt{3}}\\x-2=-\dfrac{4}{\sqrt{3}}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2+\dfrac{4}{\sqrt{3}}=2+\dfrac{4\sqrt{3}}{3}=\dfrac{6+4\sqrt{3}}{3}\\x=2-\dfrac{4}{\sqrt{3}}=\dfrac{6-4\sqrt{3}}{3}\end{matrix}\right.\)

1: \(\left|x-3,5\right|>=0\forall x\)
\(\left|4,5-y\right|>=0\forall y\)
Do đó: \(\left|x-3,5\right|+\left|4.5-y\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-3,5=0\\4,5-y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3,5\\y=4,5\end{matrix}\right.\)
2: \(\left\{{}\begin{matrix}\left|x+\dfrac{2}{3}\right|>=0\forall x\\\left|y-\dfrac{3}{4}\right|>=0\forall y\\\left|z-5\right|>=0\forall z\end{matrix}\right.\)
Do đó: \(\left|x+\dfrac{2}{3}\right|+\left|y-\dfrac{3}{4}\right|+\left|z-5\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+\dfrac{2}{3}=0\\y-\dfrac{3}{4}=0\\z-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{3}{4}\\z=5\end{matrix}\right.\)
3: \(\left|x-2\right|+\left|3-x\right|=0\)
=>|x-2|+|x-3|=0(1)
TH1: x<2
Phương trình (1) sẽ trở thành 2-x+3-x=0
=>5-2x=0
=>2x=5
=>x=2,5(loại)
TH2: 2<=x<3
Phương trình (1) sẽ trở thành x-2+3-x=0
=>1=0(loại)
TH3: x>=3
Phương trình (1) sẽ trở thành x-2+x-3=0
=>2x=5
=>x=2,5(loại)
Vậy: Phương trình vô nghiệm
4: \(\left\{{}\begin{matrix}\left|x-\dfrac{2}{3}\right|>=0\forall x\\\left|x+y+\dfrac{3}{4}\right|>=0\forall x,y\\\left|y-z-\dfrac{5}{6}\right|>=0\forall y,z\end{matrix}\right.\)
Do đó: \(\left|x-\dfrac{2}{3}\right|+\left|x+y+\dfrac{3}{4}\right|+\left|y-z-\dfrac{5}{6}\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{3}=0\\x+y+\dfrac{3}{4}=0\\y-z-\dfrac{5}{6}=0\end{matrix}\right.\)
=>\(\begin{matrix}x=\dfrac{2}{3}\\y=-x-\dfrac{3}{4}=-\dfrac{2}{3}-\dfrac{3}{4}=\dfrac{-17}{12}\\z=y-\dfrac{5}{6}=-\dfrac{17}{12}-\dfrac{5}{6}=-\dfrac{27}{12}=-\dfrac{9}{4}\end{matrix}\)
5: \(\left\{{}\begin{matrix}\left|x-\dfrac{2}{3}\right|>=0\forall x\\\left|xy-\dfrac{5}{8}\right|>=0\forall x,y\\\left|yz+\dfrac{3}{4}\right|>=0\forall y,z\end{matrix}\right.\)
Do đó: \(\left|x-\dfrac{2}{3}\right|+\left|xy-\dfrac{5}{8}\right|+\left|yz+\dfrac{3}{4}\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{3}=0\\xy-\dfrac{5}{8}=0\\yz+\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\xy=\dfrac{5}{8}\\yz=-\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{5}{8}:x=\dfrac{5}{8}:\dfrac{2}{3}=\dfrac{5}{8}\cdot\dfrac{3}{2}=\dfrac{15}{16}\\z=-\dfrac{3}{4}:\dfrac{15}{16}=-\dfrac{3}{4}\cdot\dfrac{16}{15}=\dfrac{-48}{60}=-\dfrac{4}{5}\end{matrix}\right.\)
6: \(\left\{{}\begin{matrix}\left|xy+\dfrac{2}{3}\right|>=0\forall x,y\\\left|yz-\dfrac{8}{9}\right|>=0\forall y,z\\\left|xz+\dfrac{3}{4}\right|>=0\forall x,z\end{matrix}\right.\)
Do đó: \(\left|xy+\dfrac{2}{3}\right|+\left|yz-\dfrac{8}{9}\right|+\left|xz+\dfrac{3}{4}\right|>=0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}xy+\dfrac{2}{3}=0\\yz-\dfrac{8}{9}=0\\xz+\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}xy=-\dfrac{2}{3}\\yz=\dfrac{8}{9}\\xz=-\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left(xyz\right)^2=-\dfrac{2}{3}\cdot\dfrac{8}{9}\cdot\dfrac{-3}{4}=\dfrac{1}{2}\cdot\dfrac{8}{9}=\dfrac{4}{9}\)
=>\(\left[{}\begin{matrix}xyz=\dfrac{2}{3}\\xyz=-\dfrac{2}{3}\end{matrix}\right.\)
TH1: xyz=2/3
=>\(\left\{{}\begin{matrix}z=\dfrac{xyz}{xy}=\dfrac{2}{3}:\dfrac{-2}{3}=-1\\x=\dfrac{xyz}{yz}=\dfrac{2}{3}:\dfrac{8}{9}=\dfrac{2}{3}\cdot\dfrac{9}{8}=\dfrac{18}{24}=\dfrac{3}{4}\\y=\dfrac{xyz}{xz}=\dfrac{2}{3}:\dfrac{-3}{4}=\dfrac{2}{3}\cdot\dfrac{4}{-3}=-\dfrac{8}{9}\end{matrix}\right.\)
TH2: xyz=-2/3
=>\(\left\{{}\begin{matrix}z=\dfrac{xyz}{xy}=-\dfrac{2}{3}:\dfrac{-2}{3}=1\\x=\dfrac{xyz}{yz}=-\dfrac{2}{3}:\dfrac{8}{9}=\dfrac{-2}{3}\cdot\dfrac{9}{8}=\dfrac{-18}{24}=\dfrac{-3}{4}\\y=\dfrac{xyz}{xz}=\dfrac{-2}{3}:\dfrac{-3}{4}=\dfrac{-2}{3}\cdot\dfrac{4}{-3}=\dfrac{8}{9}\end{matrix}\right.\)

\(\dfrac{9}{5}< 2;\dfrac{7}{6}< \dfrac{29}{24};3>\dfrac{17}{18}\)

Lời giải:
Chiều rộng khu đất: $2016:12=168$ (m)
Tổng chiều dài và chiều rộng khu đất: $102:2=51$ (m)
Bản thân chiều rộng khu đất còn lớn hơn cả tổng hai chiều, đề có vấn đề bạn xem lại nhé.
 cú ét ô ét
cú ét ô ét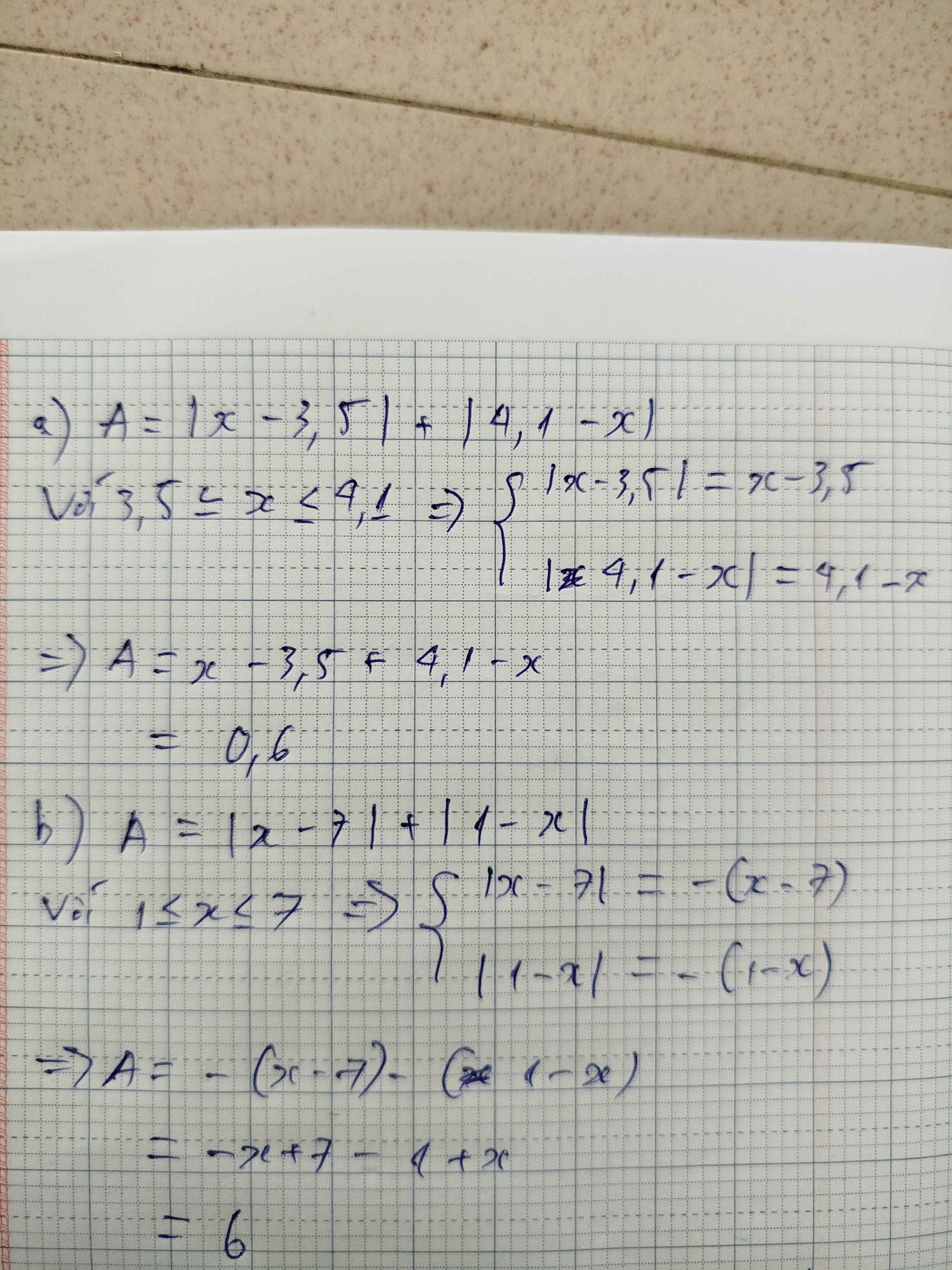
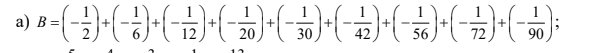

thời gian dự định là: 10h00 - 5h40 = 4h20 = 260 phút
thời gian di chuyển thực tế là: 260 - 20 = 240 (phút) = 4 giờ
quãng đường đi là: 30 x 4 = 120 (km)
quãng đường đi được trước khi bị xe hư là: 1 x 30 = 30km
quãng đường còn lại là: 120 - 30 = 90 (km)
vận tốc mới là: 30 + 10 = 40 (km/h)
thồi gian đi quãng đường còn lại là: 90 : 40 = 2,25 (giờ) = 2h15p
thời gian sửa chữa xe là: 30p = 1/2 giờ
tổng thời gian thực tế đã đi là:
1 giờ + 1/2 giờ + 2 giờ 15 phút = 3 giờ 45 phút
thời gian 2 bố con đến nơi sớm hơm dự định là:
4h20p - 3h45p = 0h35p
vậy 2 bố con đến sớm hơn 35p