tập hợp rỗng

a) đề <=> 2(x^4 +y^4+z^4)-2(x^2y^2 +y^2z^2+z^2x^2)>=0

<=>(x^2-y^2)^2 +(x^2-z^2)^2 + (y^2-z^2)^2>= 0 (đúng)

=> bất đẳng thức ở đề đúng

b) Cmtt câu a rồi suy ra (a-b)^2 + (b-c)^2 + (c-a)^2>=0

Ta có : \(\frac{x-35}{21}+\frac{x-36}{20}>\frac{x-37}{19}+\frac{x-38}{18}\)(1)

\(\Leftrightarrow\left(\frac{x-35}{21}-1\right)+\left(\frac{x-36}{20}-1\right)\)\(-\left(\frac{x-37}{19}-1\right)-\left(\frac{x-38}{18}-1\right)\)\(>0\)

\(\Leftrightarrow\frac{x-56}{21}+\frac{x-56}{20}-\frac{x-56}{19}-\frac{x-56}{18}\)\(>0\)

\(\Leftrightarrow\left(x-56\right)\left(\frac{1}{21}+\frac{1}{20}-\frac{1}{19}-\frac{1}{18}\right)\)\(>0\)

Vì \(\frac{1}{21}+\frac{1}{20}-\frac{1}{19}-\frac{1}{18}< 0\)

\(\Rightarrow x-56< 0\)\(\Leftrightarrow x< 56\)

Vậy tập nghiệm của BPT(1) là \(S=\left\{x\in R|x< 56\right\}\)

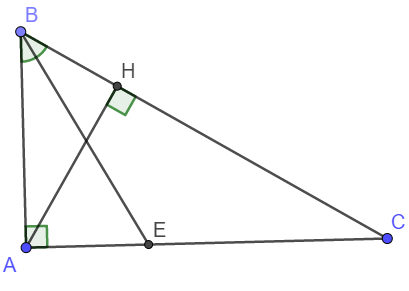
a) Xét tam giác ABC và tam giác HBA có:

\(\widehat{BAC}=\widehat{BHA}=90^o\)

Góc B chung

\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)

b) 

Xét tam giác ABC và tam giác HAC có:

\(\widehat{BAC}=\widehat{AHC}=90^o\)

Góc C chung

\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g-g\right)\)

c) Từ câu a và b ta có : \(\Delta HBA\sim\Delta HAC\)

\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB.HC=9.16=144\)

\(\Rightarrow HA=12\left(cm\right)\)

Khi đó áp dụng định lý Pi-ta-go ta có:

\(AB^2=BH^2+AH^2=9^2+12^2\Rightarrow AB=15\left(cm\right)\)

\(AC^2=CH^2+AH^2=16^2+12^2\Rightarrow AC=20\left(cm\right)\)

BC = BH + HC = 9 + 16 = 25 (cm)

Áp dụng tính chất tia phân giác trong tam giác ta có:

\(\frac{AE}{EC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}\)

\(\Rightarrow AE=\frac{3}{8}\times20=7,5\left(cm\right)\)

\(\Rightarrow EC=20-7,5=12,5\left(cm\right)\)

gọi số cần tìm là a(2a) (\(a\varepsilon N,0< a\le9\))

theo bài ra ta có :a2(2a)-a(2a)=200

=> 100a+20+2a-10a-2a=200

=>90a+20=200

=>90a=180

=>a=2

vậy số cần tìm là 24

15 phút = 1/4 giờ

Gọi độ dài quãng đường AB là x (km, x > 0)

Thời gian đi theo dự định là:    \(\frac{x}{35}\left(h\right)\)

Vận tốc nửa quãng đường sau là:  35 + 5 = 40 (km/h)

Thời gian đi theo thực tế là: \(\frac{x}{2.35}+\frac{1}{4}+\frac{x}{2.40}\)  (h)

Theo bài ra ta có phương trình:

\(\frac{x}{2.35}+\frac{1}{4}+\frac{x}{2.40}=\frac{x}{35}\)

\(\Leftrightarrow\frac{x}{35}-\frac{3x}{112}=\frac{1}{4}\)

\(\Leftrightarrow\frac{x}{560}=\frac{1}{4}\)

\(\Leftrightarrow x=140\left(tmđk\right)\)

Vậy quãng đường AB dài 140km.

Đổi 15p = 0,25h
Gọi x(h) là thời gian dự định (x > 0)
Khi đó quãng đường AB dài 35x(km)
Theo đề ra ta có 35 . x/2 = (35 + 5) . (x/2 - 0,25)
35 . x/2 = 40 . (x/2 - 0,25)
<=> 17,5x = 20x - 10
<=> 20x - 17,5x = 10
<=> 2,5x = 10
<=> x = 4
<=> 35x = 140
Vậy quãng đường AB dài 140km