Cho B=\(\dfrac{n+1}{n-2}\) , Tìm n biết B= 4, B=\(\dfrac{-1}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1-3+5-7+9-11+.......+2021-2023
=(1-3)+(5-7)+(9-11)+...+(2021-2023)
=(-2)+(-2)+(-2)+....+(-2) (có 506 số -2)
=506 x (-2)
=-1012

\(6.3\\ \dfrac{8}{-11}=\dfrac{8.\left(-1\right)}{\left(-11\right).\left(-1\right)}=\dfrac{-8}{11};\dfrac{-5}{-9}=\dfrac{-5:\left(-1\right)}{\left(-9\right):\left(-1\right)}=\dfrac{5}{9}\\ --\\ 6.4\\ \dfrac{-12}{4}=\dfrac{-12:4}{4:4}=-3\\ \dfrac{7}{-35}=\dfrac{7:\left(-7\right)}{-35:\left(-7\right)}=-\dfrac{1}{5}\\ \dfrac{-9}{27}=\dfrac{-9:9}{27:9}=\dfrac{-1}{3}\)
\(6.5\\ 15p=\dfrac{15}{60}\left(h\right)=\dfrac{15:15}{60:15}\left(h\right)=\dfrac{1}{4}\left(h\right)\\ 90p=\dfrac{90}{60}\left(h\right)=\dfrac{90:30}{60:30}\left(h\right)=\dfrac{3}{2}\left(h\right)\)

\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2024}}\\ =>2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2023}}\\ =>2A-A=A=1-\dfrac{1}{2^{2024}}=\dfrac{2^{2024}-1}{2^{2024}}\)

\(\dfrac{x}{-2}=-\dfrac{8}{x}\left(x\ne0\right)\\ =>x.x=\left(-2\right).\left(-8\right)\\ =>x^2=16\\ =>x=\pm4\)
\(\dfrac{x}{-2}=\dfrac{-8}{x}\\ x.x=\left(-8\right).\left(-2\right)=16=4.4=\left(-4\right).\left(-4\right)\\ Vậy:\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

\(\dfrac{x+3}{2015}+\dfrac{x+2}{2016}+\dfrac{x+1}{2017}+\dfrac{x}{1009}=-5\\ =>\left(\dfrac{x+3}{2015}+1\right)+\left(\dfrac{x+2}{2016}+1\right)+\left(\dfrac{x+1}{2017}+1\right)+\left(\dfrac{x}{1009}+2\right)=0\\ =>\dfrac{x+2018}{2015}+\dfrac{x+2018}{2016}+\dfrac{x+2018}{2017}+\dfrac{x+2018}{1009}=0\\ =>\left(x+2018\right)\left(\dfrac{1}{2015}+\dfrac{1}{2016}+\dfrac{1}{2017}+\dfrac{1}{1009}\right)=0\\ =>x+2018=0\\ =>x=-2018\left(TM\right)\)

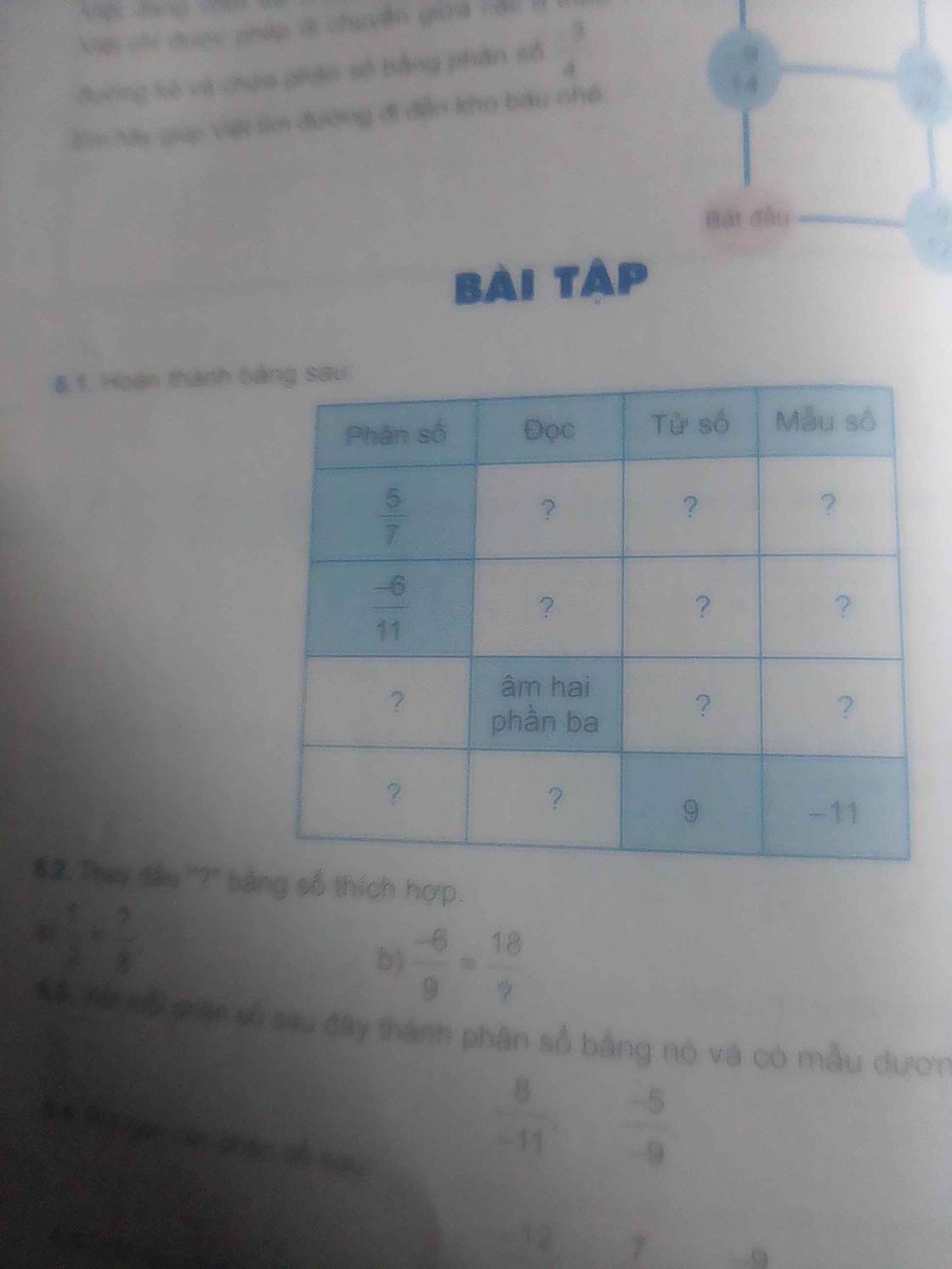
| Phân số | Đọc | Tử Số | Mẫu số |
| \(\dfrac{5}{7}\) | Năm phần bẩy | 5 | 7 |
| \(\dfrac{-6}{11}\) | âm sáu phần mười một | -6 | 11 |
| \(\dfrac{-2}{13}\) | âm hai phần ba | -2 | 13 |
| \(\dfrac{9}{-11}\) | chín phần âm mười một | 9 | -11 |

Lời giải:
$2^{x+2}.3^2-3.5^2=69$
$2^{x+3}.9=69+3.5^2=144$
$2^{x+3}=144:9=16=2^4$
$\Rightarrow x+3=4$
$\Rightarrow x=1$


Lời giải:
$\frac{1}{50}> \frac{1}{100}$
$\frac{1}{51}> \frac{1}{100}$
.....
$\frac{1}{98}> \frac{1}{100}$
$\frac{1}{99}> \frac{1}{100}$
$\Rightarrow S> \underbrace{\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}}_{50}=\frac{1}{100}.50=\frac{1}{2}$

\(B=4\Rightarrow\dfrac{n+1}{n-2}=4\)
\(\Rightarrow n+1=4\left(n-2\right)\)
\(\Rightarrow n+1=4n-8\)
\(\Rightarrow4n-n=1+8\)
\(\Rightarrow3n=9\)
\(\Rightarrow n=3\)
b.
\(B=-\dfrac{1}{2}\Rightarrow\dfrac{n+1}{n-2}=-\dfrac{1}{2}\)
\(\Rightarrow n-2=-2\left(n+1\right)\)
\(\Rightarrow n-2=-2n-2\)
\(\Rightarrow n+2n=2-2\)
\(\Rightarrow3n=0\)
\(\Rightarrow n=0\)
\(B=4\\ \Leftrightarrow\dfrac{n+1}{n-2}=4\\ \Leftrightarrow4n+4=n-2\\ \Leftrightarrow4n-n=-2-4\\ \Leftrightarrow3n=-6\\ \Leftrightarrow n=-2\\ B=\dfrac{-1}{2}\\ \Leftrightarrow\dfrac{n+1}{n-2}=\dfrac{-1}{2}\\ \Leftrightarrow2n+2=-n+2\\ \Leftrightarrow2x+n=2-2\\ \Leftrightarrow3n=0\\ \Leftrightarrow n=0\)