. Cho tam giác ABC vuông cân tại A. Giả sử D là điểm nằm bên trong tam giác sao cho tam giác ABD cân và ADB = 150o. Trên nửa mặt phẳng không chứa D có bờ là đường thẳng AC lấy điểm E sao cho tam giác ACE đều. Chứng minh 3 điểm B, D, E thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(15x-3^2.x-6x=6978\left(17-34:2\right)\\ \Rightarrow15x-9x-6x=6978\left(17-17\right)\\ \Rightarrow\left(15-9-6\right).x=6978.0\\ \Rightarrow0x=0\) (luôn đúng với mọi giá trị của x)
Vậy có vô số giá trị x thỏa mãn đề bài.
333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333

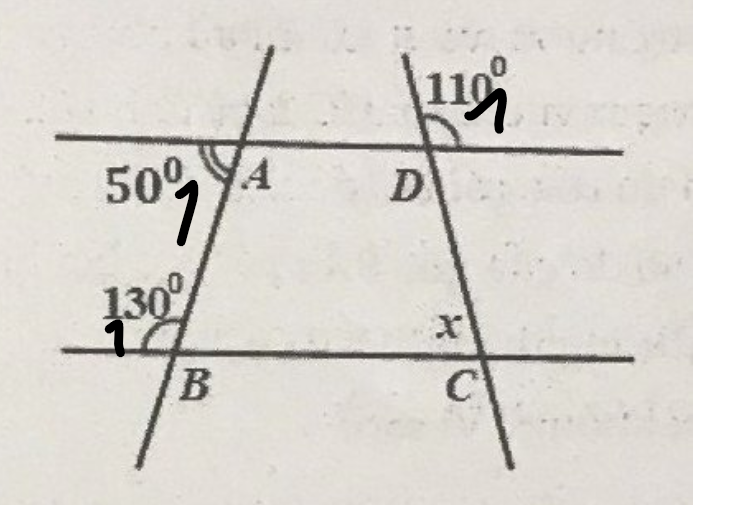
\(\widehat{A_1}+\widehat{BAD}=180^0\)
=>\(\widehat{BAD}+50^0=180^0\)
=>\(\widehat{BAD}=130^0\)
Ta có: \(\widehat{ADC}=\widehat{D_1}\)(hai góc đối đỉnh)
=>\(\widehat{ADC}=110^0\)
Ta có: \(\widehat{BAD}=\widehat{B_1}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
=>\(\widehat{ADC}+\widehat{DCB}=180^0\)
=>\(x+110^0=180^0\)
=>\(x=70^0\)
b)
\(\widehat{B}+\widehat{A}=130^o+50^o=180^o\)
Mà 2 góc này ở vị trí trong cùng phía
\(\Rightarrow BC//AD\Rightarrow\widehat{D}+\widehat{C}=180^o\)
\(\widehat{D}=110^o\) (đối đỉnh)
\(\Rightarrow\widehat{C}=180^o-110^o=70^o\)

Giải:
Số các số chẵn từ 16 đến 52 là:
(52 - 16) : 2 + 1 = 19 (số)
Đáp số: 19 số

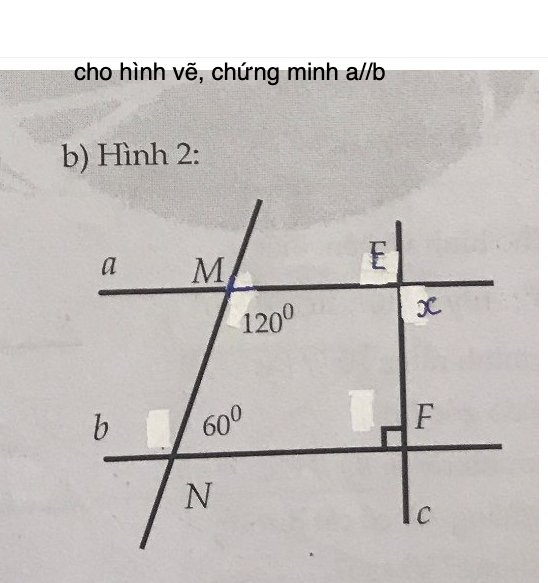
Ta có: \(\widehat{xMN}+\widehat{MNF}=120^0+60^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên a//b

Giải:
Chiều dài lúc sau bằng: 1 - \(\dfrac{2}{5}\) = \(\dfrac{3}{5}\) (chiều dài lúc đầu)
Chiều rộng lúc sau bằng: 1 + \(\dfrac{4}{7}\) = \(\dfrac{11}{7}\) (chiều rôngj lúc đầu)
Tỉ số chiều dài lúc đầu và chiều rộng lúc đầu là"
\(\dfrac{11}{7}\) : \(\dfrac{3}{5}\) = \(\dfrac{55}{21}\)
Nử chu vi hình chữ nhật ban đầu là:
760 : 2 = 380 (m)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Chiều dài lúc đầu là: 380: (55 + 21) x 55 = 275 (m)
Chiều rộng lúc đầu là: 380 - 275 = 105 (m)
Diện tich thửa ruộng lúc đầu là" 275 x 105 = 28875 (m2)
Thửa ruộng đó thu được số ki-lô-gam thóc là:
4 x 28875 : 5 = 23100 (kg)
Đáp số: 23100 kg

ĐKXĐ: \(a\ne1\)
Để A là số nguyên thì \(a^3+2⋮a-1\)
=>\(a^3-1+3⋮a-1\)
=>\(3⋮a-1\)
=>\(a-1\in\left\{1;-1;3;-3\right\}\)
=>\(a\in\left\{2;0;4;-2\right\}\)

Gọi số cần tìm có dạng là \(\overline{3abc}\)
Theo đề, ta có: \(\overline{3abc}-3000=\dfrac{\overline{3abc}}{9}\)
=>\(\overline{abc}=\dfrac{3000+\overline{abc}}{9}\)
=>\(9\overline{abc}=3000+\overline{abc}\)
=>\(8\overline{abc}=3000\)
=>\(\overline{abc}=375\)
Vậy: Số cần tìm là 3375
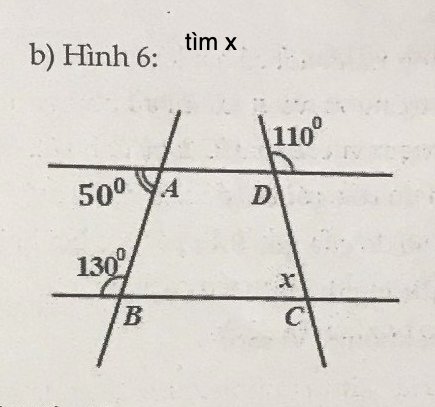
Tam giác ACE đều \(\Rightarrow AE=AC\) và \(\widehat{CAE}=60^o\)
Tam giác ABC vuông cân tại A \(\Rightarrow AB=AC\) và \(\widehat{BAC}=90^o\)
Từ đó \(\Rightarrow AE=AB\) \(\Rightarrow\Delta ABE\) cân tại A
Đồng thời \(\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=90^o+60^o=150^o\)
\(\Rightarrow\widehat{ABE}=\dfrac{180^o-\widehat{BAE}}{2}=\dfrac{180^o-150^o}{2}=15^o\)
Mặt khác, tam giác ADB cân tại và \(\widehat{ADB}=150^o\) nên tam giác ADB chí có thể cân tại D (vì nếu cân tại điểm khác thì khi đó trong tam giác ADB sẽ có 2 góc bằng \(150^o\), vô lý). Khi đó \(\widehat{ABD}=15^o\)
Trên cùng 1 nửa mặt phẳng bờ là đường thẳng chứa tia BA, có \(\widehat{ABD}=\widehat{ABE}=15^o\) nên B, D, E thẳng hàng. (đpcm)