Gọi số hàng dọc nhiều nhất có thể chia là x

⇒ x = ƯCLN(36; 32; 48) 

Ta có:

\(36=2^2\cdot3^2\)

\(32=2^5\)

\(48=2^4\cdot3\)

\(\Rightarrow x=ƯCLN\left(36;32;48\right)=2^2=4\) (hàng)  

Vậy: ... 

Giải:

a, đa thức tính diện tích mảnh đất trồng rau là:

       S = \(x.x\) (m²)

        S = \(x^2\)   (m²)

b,Theo bài ra ta có: \(x^2\) = 96

                           \(\)  \(\left[{}\begin{matrix}x=4\sqrt{6}\\x=-4\sqrt{6}\end{matrix}\right.\)

                            Vì \(x\) > 0 nên \(x\) = 4\(\sqrt{6}\)

Kết luận: cạnh của khu vườn có độ dài là: 4\(\sqrt{6}\)(m)

a) 16 = 2⁴

24 = 2³.3

⇒ ƯCLN(16; 24) = 2³ = 8

⇒ ƯC(16; 24) = Ư(8) = {1; 2; 4; 8}

b) 84 = 2².3.7

108 = 2².3³

⇒ BCNN(84; 108) = 2².3³.7= 756

⇒ BC(84; 108) = B(756) = {0; 756; 1512; ...}

\(\left(x-3\right)\left(y-3\right)=9\) 

\(\Rightarrow x-3,y-3\inƯ\left(9\right)\)

Ta có bảng:

Vậy: ...

a) Ta có:

∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠BAC = 180⁰ - ∠B - ∠C

= 180⁰ - 73⁰ - 45⁰ = 62⁰

⇒ ∠A₁ = ∠A₂ = 62⁰ : 2

= 21⁰

⇒ x = 180⁰ - ∠B - ∠A₁

= 180⁰ - 73⁰ - 31⁰

= 76⁰

y = 180⁰ - ∠C - ∠A₂

= 180⁰ - 45⁰ - 31⁰

= 104⁰

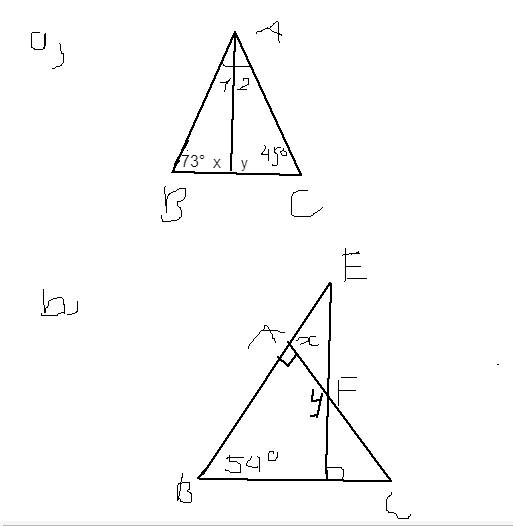
b)

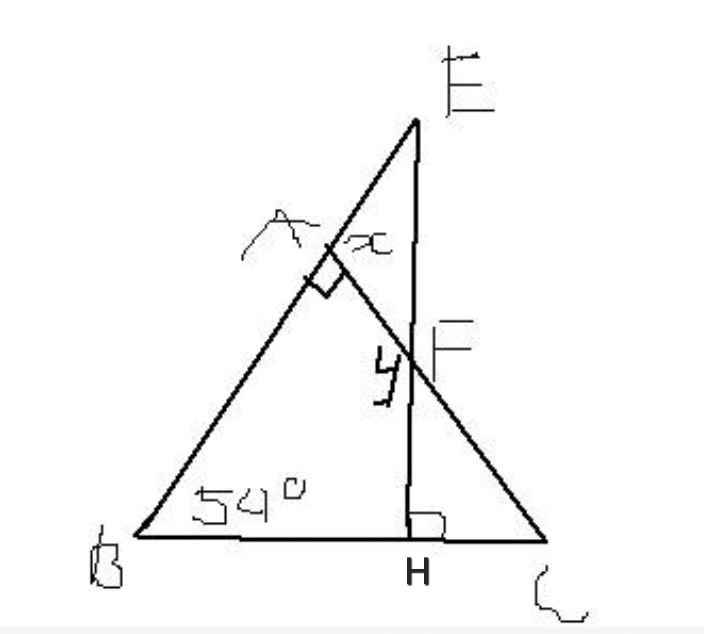
Ta có:

∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠C = 180⁰ - ∠BAC - ∠B

= 180⁰ - 54⁰ - 90⁰

= 36⁰

Ta có:

∠C + ∠CFH + ∠CHF = 180⁰ (tổng ba góc trong ∆CHF)

⇒ ∠CFH = 180⁰ - ∠C - ∠CHF

= 180⁰ - 36⁰ - 90⁰

= 54⁰

Ta có:

y + ∠CFH = 180⁰ (kề bù)

⇒ y = 180⁰ - 54⁰

= 126⁰

x là góc nào em?

Ta có:

\(a=45=3^2\cdot5\)

\(b=204=2^2\cdot3\cdot17\)

\(b=2\cdot3^2\cdot7\)

\(\Rightarrow\text{Ư}CLN\left(a,b,c\right)=3\)

a=45; b= 204; c=126. Tìm ƯCLN(a,b,c)

Ta có: 45 = 3². 5; 204 = 2² .3. 17; 126 = 2 . 3² .7

Thừa số nguyên tố chung là: 3

=> ƯCLN(a,b,c) = ƯCLN(45,204;126) = 3

Vậy ƯCLN(a,b,c) = 3

31¹¹ < 32¹¹ = (2⁵)¹¹ = 2⁵⁵

17¹⁴ > 16¹⁴ = (2⁴)¹⁴ = 2⁵⁶

Vì 2⁵⁵ < 2⁵⁶ nên 31¹¹ < 17¹⁴

Đáp án:

 17 mũ 14 > 31 mũ 11

Giải thích các bước giải:

 ta có :

31 mũ 11 < 32 mũ 11 =  ( 2 mũ 5 ) mũ 11 = 2 mũ 55

17 mũ 14 > 16 mũ 14 = ( 2 mũ 4 ) mũ 14 = 2 mũ 56

ta thấy 2 mũ 56 > 2 mũ 55 nên 17 mũ 14 > 31 mũ 11

Chữ số 2 trong 45,329 có giá trị là : \(0,02=\dfrac{2}{100}\)

Chữ số 2 trong số thập phân 45,329 có giá trị là 0,02

   2⁹¹ và 5³⁶

 2⁹¹=  (2⁵)¹⁸.2 = 32¹⁸.2 

 5³⁶ = (5²)¹⁸    = 25¹⁸

 32 > 25 ⇒ 32¹⁸ > 25¹⁸ ⇒ 2⁹¹ > 5³⁶

\(2^{91}>2^{90}\)

Ta có:

\(2^{90}=\left(2^5\right)^{18}=32^{18}\)

\(5^{36}=\left(5^2\right)^{18}=25^{18}\)

Mà: \(32>25\)

\(\Rightarrow32^{18}>25^{18}\)

\(\Rightarrow2^{90}>5^{36}\)

\(\Rightarrow2^{91}>5^{36}\)

Ta có:

\(2^{91}>2^{90}=\left(2^5\right)^{18}=32^{18}>25^{18}=\left(5^2\right)^{18}=5^{2.18}=5^{36}\)

Vậy \(2^{91}>5^{36}\).