Ta có: 27n_Al + 56n_Fe = 11 (1)

\(n_{SO_2}=0,45\left(mol\right)\)

BT e, có: \(3n_{Al}+3n_{Fe}=2n_{SO_2}=0,9\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{Al}=0,2\left(mol\right)\\n_{Fe}=0,1\left(mol\right)\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,2.27}{11}.100\%\approx49,09\%\\\%m_{Fe}\approx50,91\%\end{matrix}\right.\)

354 + 123 477

345+123=468

Xét 3 số TN liên tiếp \(\left(n-1\right);n;\left(n+1\right)\) ta có

\(\left(n-1\right).n.\left(n+1\right)=n.\left(n^2-1\right)=n^3-n< n^3\)

\(\Rightarrow A\le\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{20.21.22}=\)

\(=\dfrac{1}{2}\left(\dfrac{3-1}{1.2.3}+\dfrac{4-2}{2.3.4}+\dfrac{5-3}{3.4.5}+...+\dfrac{22-20}{20.21.22}\right)=\)

\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{20.21}-\dfrac{1}{21.22}\right)=\)

\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{21.22}\right)=\dfrac{1}{2^2}-\dfrac{1}{2.21.22}< \dfrac{1}{2^2}\)

Trong 3 tuần, nhà máy lắp ráp được số xe đạp là :
                  320819 x 3 = 962754 (xe)
                       Đáp số: 962754 xe.

Trong 3 tuần, nhà máy lắp ráp được số xe đạp là :
                  320819 x 3 = 962754 (xe)
                       Đáp số: 962754 xe

Số trung bình cộng của một dãy số trong toán học chính là tỉ số giữa tổng giá trị của tập hợp số đó và toàn bộ các phân tử có trong tập hợp đó. Hiểu một cách đơn giản nhất về khái niệm trung bình cộng đó là thương giữa tổng các số hạng có trong dãy số đã cho với các số hạng vừa lấy tổng.

Trung bình cộng là tổng của các số cộng lại và chia cho số số hạng

VD: Trung bình cộng của 3; 5 và 7 là: \(\left(3+5+7\right):3=5\) Vậy TBC 3; 5 và 7 = 5

x + 98 = 100

x         = 100 - 98

x         = 2

1082 - x = 756

           x = 1082 - 756

           x = 326

x + 98 = 100

x = 100 - 98

x = 2

------

1082 - x = 756

x = 1082 - 756

x = 326

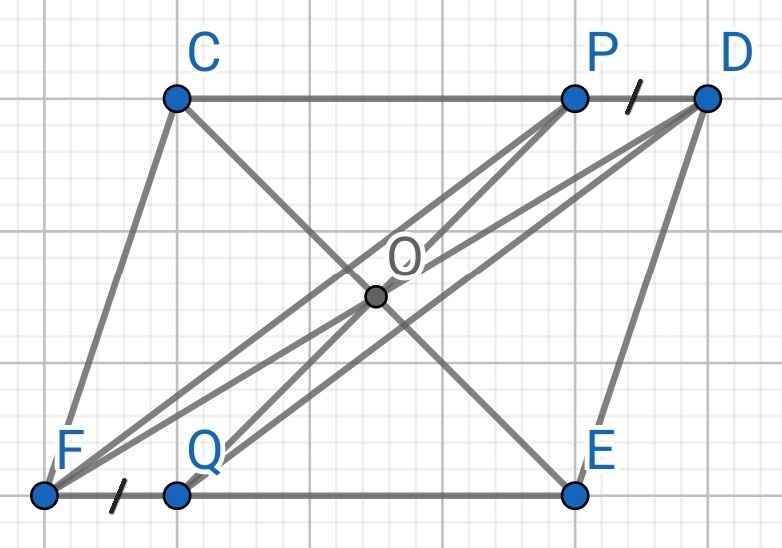 a) Sửa đề: Chứng minh PF // DQ

Do CDEF là hình bình hành (gt)

⇒ CD // EF

⇒ DP // FQ

Tứ giác DPFQ có:

DP // FQ (cmt)

DP = FQ (gt)

⇒ DPFQ là hình bình hành

⇒ PF // DQ

b) Do CDEF là hình bình hành (gt)

O là trung điểm của CE (gt)

⇒ O là trung điểm của DF

Mà DPFQ là hình bình hành

⇒ O là trung điểm của PQ