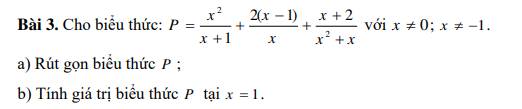
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A+\dfrac{1}{x+1}=\dfrac{3x+1}{x^2-2x+1}-\dfrac{x+3}{x^2-1}\left(x\ne\pm1\right)\)
\(A=\dfrac{3x+1}{\left(x-1\right)^2}-\dfrac{x+3}{\left(x+1\right)\left(x-1\right)}-\dfrac{1}{x+1}\)
\(A=\dfrac{\left(3x+1\right)\left(x+1\right)}{\left(x-1\right)^2\left(x+1\right)}-\dfrac{\left(x+3\right)\left(x-1\right)}{\left(x-1\right)^2\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{3x^2+3x+x+1-x^2+x-3x+3-x^2+2x-1}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{x^2+4x+3}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{x+3}{\left(x-1\right)^2}\)
\(A=\dfrac{x+3}{x^2-2x+1}\)
b) \(\dfrac{4}{x^2+x+1}-P=\dfrac{2}{1-x}+\dfrac{2x^2+4x}{x^3-1}\)
\(P=\dfrac{4}{x^2+x+1}-\dfrac{2}{1-x}-\dfrac{2x^2+4x}{x^3-1}\)
\(P=\dfrac{4}{x^2+x+1}+\dfrac{2}{x-1}-\dfrac{2x^2+4x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{4\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{2x^2+4x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{4x-4+2x^2+2x+2-2x^2-4x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2x-2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2}{x^2+x+1}\)

a, \(\dfrac{x+3}{3x-3}\) + \(\dfrac{2-x}{4x-4}\)
đkxđ: \(\left\{{}\begin{matrix}3x-3\ne0\\4x-4\ne0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}3.\left(x-1\right)\ne0\\4.\left(x-1\right)\ne0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x-1\ne0\\x-1\ne0\end{matrix}\right.\) ⇒ \(x\) ≠1
A = \(\dfrac{x+3}{3x-3}\) + \(\dfrac{2-x}{4x-4}\)
A = \(\dfrac{x+3}{3.\left(x-1\right)}\) + \(\dfrac{2-x}{4.\left(x-1\right)}\)
A = \(\dfrac{4.\left(x+3\right)}{4.3.\left(x-1\right)}\) + \(\dfrac{3.\left(2-x\right)}{3.4.\left(x-1\right)}\)
A = \(\dfrac{4x+12}{12\left(x-1\right)}\) + \(\dfrac{6-3x}{12\left(x-1\right)}\)
A = \(\dfrac{4x+12+6-3x}{12\left(x-1\right)}\)
A = \(\dfrac{\left(4x-3x\right)+\left(12+6\right)}{12\left(x-1\right)}\)
A = \(\dfrac{x+18}{12.\left(x-1\right)}\)
b, \(\dfrac{3}{x+2}-\dfrac{6}{x-1}\)
Đkxđ: \(\left\{{}\begin{matrix}x+2\ne0\\x-1\ne0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x\ne-2\\x\ne1\end{matrix}\right.\)
B = \(\dfrac{3}{x+2}\) - \(\dfrac{6}{x-1}\)
B = \(\dfrac{3.\left(x-1\right)}{\left(x+2\right)\left(x-1\right)}\) - \(\dfrac{6.\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}\)
B = \(\dfrac{3x-3}{\left(x+2\right)\left(x-1\right)}\) - \(\dfrac{6x+12}{\left(x-1\right)\left(x+2\right)}\)
B = \(\dfrac{3x-3-\left(6x+12\right)}{\left(x+2\right)\left(x-1\right)}\)
B = \(\dfrac{3x-3-6x-12}{\left(x+2\right)\left(x-1\right)}\)
B = \(\dfrac{\left(3x-6x\right)-\left(12+3\right)}{\left(x+2\right)\left(x-1\right)}\)
B = \(\dfrac{-3x-15}{\left(x+2\right)\left(x-1\right)}\)

\(A=\left\{-9;-8;-7;...;-1;0;1;2;...;8;9;10\right\}\)
Tổng các phần từ của tập hợp này:
(-9+9) + (-8+8) + (-7+7) +...+ (-1+1) + 0 + 10=10

a, A2: O2
⇒ A1 = 158 (g/mol) → A1 là KMnO4
⇒ A4 = 12 (g/mol) → A4 là C
A3: H2O
⇒ A5 = 56 (g/mol) → A5 là Fe.
b, Vai trò của:
- H2O: Do Fe pư với O2 tạo hạt chất rắn nóng chảy nhiệt độ cao (Fe3O4), khi rơi xuống bình thủy tinh có thể làm nứt bình → dùng H2O để ngăn cách Fe3O4 rơi xuống với đáy bình thủy tinh.
- C: Pư giữa Fe và O2 cần nhiệt độ cao → C cháy trước tạo nhiệt độ cho pư xảy ra.


Số cái coffee còn lại là:
\(78-2=76\) (cái coffee)
Đáp số: 76 cái coffee
Minh mua 2 cái, thế hai bạn kia có mua không?
Nếu mua thì mỗi người mua cụ thể là bao nhiêu cái?
Trước đó cả ba bạn đã có cái nào hay chưa?
Từ những lập luận trên ta có việc ba bạn có tất cả bao nhiêu cái coffee là chưa thể xác định em nhé?





 giúp mình với ạ
giúp mình với ạ

Bài 3:
a, rút gọn P = \(\dfrac{x^2}{x+1}\) + \(\dfrac{2.\left(x-1\right)}{x}\) + \(\dfrac{x+2}{x^2+x}\) với \(x\ne0;x\ne-1\)
P = \(\dfrac{x^2}{x+1}\) + \(\dfrac{2\left(x-1\right)}{x}\) + \(\dfrac{x+2}{x.\left(x+1\right)}\)
P = \(\dfrac{x^2.x}{\left(x+1\right).x}\) + \(\dfrac{2\left(x-1\right)\left(x+1\right)}{x.\left(x+1\right)}\) + \(\dfrac{x+2}{x\left(x+1\right)}\)
P = \(\dfrac{x^3}{x\left(x+1\right)}\) + \(\dfrac{2\left(x^2-1\right)}{x\left(x+1\right)}\) + \(\dfrac{x+2}{x\left(x+1\right)}\)
P = \(\dfrac{x^3+2x^2-2+x+2}{x.\left(x+1\right)}\)
P = \(\dfrac{x^3+2x^2+x-\left(2-2\right)}{x.\left(x+1\right)}\)
P = \(\dfrac{x^3+2x^2+x}{x.\left(x+1\right)}\)
P = \(\dfrac{x\left(x^2+2x+1\right)}{x.\left(x+1\right)}\)
P = \(\dfrac{x.\left(x+1\right)^2}{x.\left(x+1\right)}\)
P = \(x\) + 1
b, Thay \(x\) = 1 vào biểu thức P = \(x\) + 1 ta có:
P = 1 + 1
P = 2