Cho các số a,b thỏa mãn a3 + b3 - 6ab = -11. Chứng minh răng -\(\dfrac{7}{3}\)<a + b < -2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em. Cảm ơn em đã tin tưởng và đồng hành cùng olm trong suốt thời gian qua. Với dạng này em làm như sau nhé:
Gọi số học sinh của khối đó là \(x\) (học sinh) 0 < \(x\) < 300; \(x\) \(\in\) N
Theo bài ra ta có: ( \(x\) + 2) \(⋮\) 4; 5; 6
⇒ (\(x\) + 2) \(\in\) BC(4; 5; 6)
4 = 22; 5 = 5; 6 = 2.3 ⇒ BCNN(4; 5;6) = 22.3.5 = 60
⇒ BC(4;5;6) = {0; 60; 120; 180; 240; 300; 360; 420; ...;}
Vì 0< \(x\) < 300 ⇒0< \(x\) + 2 < 300 + 2 ⇒ 2 < \(x\) + 2 < 302
⇒ \(x\) + 2 \(\in\){60; 120; 180; 240; 300}
Lập bảng ta có:
| \(x+2\) | 60 | 120 | 180 | 240 | 300 |
| \(x\) | 58 | 118 | 178 | 238 | 298 |
Vậy \(x\) \(\in\){58; 118; 178; 238; 298}
Gọi số học sinh của khối đó là �x (học sinh) 0 < �x < 300; �x ∈∈ N
Theo bài ra ta có: ( �x + 2) ⋮⋮ 4; 5; 6
⇒ (�x + 2) ∈∈ BC(4; 5; 6)
4 = 22; 5 = 5; 6 = 2.3 ⇒ BCNN(4; 5;6) = 22.3.5 = 60
⇒ BC(4;5;6) = {0; 60; 120; 180; 240; 300; 360; 420; ...;}
Vì 0< �x < 300 ⇒0< �x + 2 < 300 + 2 ⇒ 2 < �x + 2 < 302
⇒ �x + 2 ∈∈{60; 120; 180; 240; 300}
Lập bảng ta có:
| �+2x+2 | 60 | 120 | 180 | 240 | 300 |
| �x | 58 | 118 | 178 | 238 | 298 |
Vậy �x ∈∈{58; 118; 178; 238; 298}

Physical exercises are indeed highly beneficial to our health. Regular physical activity can help protect us from serious diseases such as obesity, heart disease, cancer, mental illness, diabetes, and arthritis. Riding your bicycle regularly is one of the best ways to reduce your risk of health problems associated with a sedentary lifestyle.
Regular exercise can help protect you from heart disease and stroke, high blood pressure, noninsulin-dependent diabetes, obesity, back pain, osteoporosis, and can improve your mood and help you to better manage stress.
In conclusion, I would say that physical exercise is not only important for your body’s health but also for your mind. So, it’s important to take some time out of your busy schedule to exercise and keep yourself fit and healthy. It’s never too late to start exercising, and you don’t have to be an athlete. Even taking a brisk walk for 30 minutes a day can make a big difference. Once you do start, you’ll notice that you’ll have more energy and will be in a better mood. Physical activity reduces stress and anxiety, boosts your mood, and overall makes you feel better. So, keep exercising and stay healthy!

Để nguyên sao sáng trên trời là mộc (sao mộc)
Bỏ nặng thêm sắc là thành mốc (hỏng vứt đi)
Bớt đi chữ m ở đầu thì thành ốc (con ốc chui dưới ao)
Từ khi bỏ nặng thêm sắc là từ mốc em nhé
Để nguyên sao sáng trên trời là mộc (sao mộc)
Bỏ nặng thêm sắc là thành mốc (hỏng vứt đi)
Bớt đi chữ m ở đầu thì thành ốc (con ốc chui dưới ao)
Từ khi bỏ nặng thêm sắc là từ mốc

Olm cảm ơn em vì đã đồng hành cùng olm trong suốt thời gian qua.
Bài thơ em chia sẻ rất hay và ý nghĩa, xin cảm ơn em.
Bài thơ này tác giả là ai vậy em nhỉ? Một bài thơ rất tuyệt vời, giàu cảm xúc, chân thực đậm tình cảm thầy trò em nhé!
Một lần nữa cảm ơn em.
Cô Thương Hoài thưởng em 20 gp vì bài thơ mà em đã chia sẻ trên olm. Thân mến!

Olm cảm ơn em, bài thơ rất hay và giàu cảm xúc, chân thực và sâu lắng. Chúc em học tập hiệu quả và vui vẻ cùng olm.

Olm chào em, cảm ơn em đã đồng hành cùng olm. Khi làm bài luyện trên olm thì em cần chú ý đọc kỹ đề, đề yêu cầu gì thì trả lời cái đó. Nắm vững kiến thức cơ bản để vận dụng làm bài tập thì em sẽ chọn đúng đáp án của bài toán.
Chúc em học tập hiệu quả cùng olm, thân mến!

A B C E O D H M N
a/
Xét tg ABD và tg ACE có
\(\widehat{BAC}\) chung
\(\widehat{ABD}=\widehat{ACE}\) (góc nội tiếp cùng chắn cung DE)
=> tg ABD đồng dạng với tg ACE (g.g.g)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\Rightarrow AD.AC=AE.AB\)
b/
\(\widehat{BEC}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow CE\perp AB\)
\(\widehat{BDC}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow BD\perp AC\)
=> H là trực tâm của tg ABC \(\Rightarrow AH\perp BC\) (trong tg 3 đường cao đồng quy)

a) Tứ giác BCDE nội tiếp nên \(\widehat{ABD}=\widehat{ACE}\). Từ đó dễ dàng chứng minh \(\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrow AD.AC=AB.AE\) (đpcm)
b) Đường tròn (O) có đường kính BC nên \(\widehat{BEC}=\widehat{BDC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow BD\perp AC,CE\perp AB\) \(\Rightarrow\) H là trực tâm tam giác ABC
\(\Rightarrow AH\perp BC\) (đpcm)
c) Hạ \(HS\perp AO\) tại S. \(\Rightarrow S\in\left(AH\right)\). Khi đó tứ giác OKHS nội tiếp nên \(AS.AO=AH.AK=AD.AC=AN^2\) .
Từ đây dễ dàng chứng minh \(\Delta ASN~\Delta ANO\left(c.g.c\right)\) \(\Rightarrow\widehat{ASN}=\widehat{ANO}\). Ta có \(\widehat{ANO}=90^o\Rightarrow\widehat{ASN}=90^o\) hay \(SN\perp AO\) tại S
Hoàn toàn tương tự, ta chứng minh được \(SM\perp AO\) tại S
Lại có \(HS\perp AO\) tại S nên H, M, N thẳng hàng (đpcm).

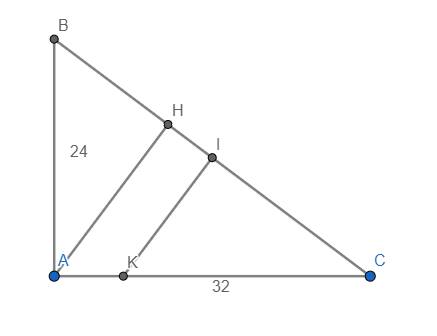
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\))
Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)
Nên \(\widehat{HAC}\approx53,13^o\)
Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm
\(\Rightarrow IB=IC=20cm\)
Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)
Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)
Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)
\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)
Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)
Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)
\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)


