 giải đầy đủ giúp em với ạ, em cảm ơn ạ.
giải đầy đủ giúp em với ạ, em cảm ơn ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Mỗi số lẻ liên tiếp cách nhau 2 đơn vị mà đây là dãy tăng dần nên:
a = 17 + 2 = 19
b = 19 + 2 = 21
b) Mỗi số tự nhiên liên tiếp cách nhau 1 đơn vị mà đây là dãy giảm dần nên:
m = 101 + 1 = 102
n = 101 - 1 = 100
p = 100 - 1 = 99
Ta có:
2020 < 2021
a) Nếu a > 2021 thì a > 2020
b) a < 2020

2B:
a) C1: \(\dfrac{-7}{12}=\dfrac{-6-1}{12}=\dfrac{-6}{12}+\dfrac{-1}{12}=\dfrac{-1}{2}+\dfrac{-1}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{-3-4}{12}=\dfrac{-3}{12}+\dfrac{-4}{12}=\dfrac{-1}{4}+\dfrac{-1}{3}\)
C4: \(\dfrac{-7}{12}=\dfrac{-2-5}{12}=\dfrac{-2}{12}+\dfrac{-5}{12}\)
b) C1: \(\dfrac{-7}{12}=\dfrac{4-11}{12}=\dfrac{4}{12}-\dfrac{11}{12}=\dfrac{1}{3}-\dfrac{11}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{2-9}{12}=\dfrac{2}{12}-\dfrac{9}{12}=\dfrac{1}{6}-\dfrac{3}{4}\)
C3: \(\dfrac{-7}{12}=\dfrac{3-10}{12}=\dfrac{3}{12}-\dfrac{10}{12}=\dfrac{1}{4}-\dfrac{5}{6}\)

Bài 1B:
a)
\(\dfrac{-1}{16}+\dfrac{-1}{24}\\ =\dfrac{-3}{48}+\dfrac{-2}{48}\\ =\dfrac{-5}{48}\)
b)
\(\dfrac{-1}{8}-\dfrac{3}{20}\\ =\dfrac{-5}{40}-\dfrac{6}{40}\\ =\dfrac{-11}{40}\)
c)
\(-\dfrac{18}{10}+0,4\\ =\dfrac{-9}{5}+\dfrac{2}{5}\\ =\dfrac{-7}{5}\)
d)
\(6,5-\left(-\dfrac{1}{5}\right)\\ =\dfrac{13}{2}+\dfrac{1}{5}\\ =\dfrac{65}{10}+\dfrac{2}{10}\\ =\dfrac{67}{10}\)

\(A=\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\\ 2A=1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\\ 2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\right)-\left(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\right)\\ A=1+\left(\dfrac{2}{2}-\dfrac{1}{2}\right)+\left(\dfrac{3}{2^2}-\dfrac{2}{2^2}\right)+...+\left(\dfrac{2023}{2^{2022}}-\dfrac{2022}{2^{2022}}\right)+\dfrac{2023}{2^{2023}}\\ A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}+\dfrac{2023}{2^{2023}}\\ 2A=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2021}}+\dfrac{2023}{2^{2023}}\\ 2A-A=\left(3+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{2023}{2^{2023}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}\right)\\ A=\left(3-1\right)+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{2^2}-\dfrac{1}{2^2}\right)+...+\left(\dfrac{1}{2^{2021}}-\dfrac{1}{2^{2021}}\right)-\dfrac{2023}{2^{2023}}-\dfrac{1}{2^{2022}}\\ A=2-\dfrac{2023+2}{2^{2023}}\\ A=2-\dfrac{2025}{2^{2023}}< 2\\ \)
@ Phong Lần sau em nên chú ý về dấu như vậy bài làm sẽ hoàn hảo em nhé!

Gọi ba số tự nhiên liên tiếp là a;a+1;a+2
Tổng của ba số là 264 nên a+a+1+a+2=264
=>3a=261
=>a=261:3=87
Vậy: Ba số tự nhiên liên tiếp cần tìm là 87;87+1=88;87+2=89

Gọi ba số tự nhiên chẵn liên tiếp là a;a+2;a+4
Tổng của số lớn nhất và số bé nhất là 644 nên a+a+4=644
=>2a=640
=>a=320
Vậy: ba số cần tìm là 320;320+2=322;320+4=324

Tổng số tuổi của hai mẹ con hiện tại là:
34+5+5=44(tuổi)
Tổng số phần bằng nhau là 2+9=11(phần)
Tuổi con là 44:11x2=8(tuổi)
Tuổi mẹ là 44-8=36(tuổi)
Giải:
Tuổi của mẹ và tuổi con hiện nay là:
34 + 5 x 2 = 44 (tuổi)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Tuổi mẹ hiện nay là:
44 : (2 + 9) x 9 = 36 (tuổi)
Tuổi con hiện nay là:
44 - 36 = 8 (tuổi)
Đáp số: Tuổi con hiện nay là 8 tuổi
Tuổi mẹ hiện nay là 36 tuổi

a: ta có: \(\widehat{KAC}+\widehat{KAB}=\widehat{BAC}=90^0\)
\(\widehat{KAB}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)
Do đó: \(\widehat{KAC}=\widehat{HBA}\)
Xét ΔKAC vuông tại K và ΔHBA vuông tại H có
AC=BA
\(\widehat{KAC}=\widehat{HBA}\)
Do đó: ΔKAC=ΔHBA
=>AK=BH
b: Ta có: ΔABC vuông cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Ta có: \(\widehat{HAM}+\widehat{HEM}=90^0\)(ΔEMA vuông tại E)
\(\widehat{HBM}+\widehat{AEB}=90^0\)(ΔEHB vuông tại H)
=>\(\widehat{HBM}=\widehat{HAM}=\widehat{KAM}\)
c: Xét ΔEHB vuông tại H và ΔEMA vuông tại M có
\(\widehat{HEB}\) chung
Do đó: ΔEHB~ΔEMA
=>\(\dfrac{EH}{EM}=\dfrac{EB}{EA}\)
=>\(\dfrac{EH}{EB}=\dfrac{EM}{EA}\)
Xét ΔEHM và ΔEBA có
\(\dfrac{EH}{EB}=\dfrac{EM}{EA}\)
\(\widehat{HEM}\) chung
Do đó: ΔEHM~ΔEBA
=>\(\widehat{EHM}=\widehat{EBA}=45^0\)
Xét tứ giác AMKC có \(\widehat{AMC}=\widehat{AKC}=90^0\)
nên AMKC là tứ giác nội tiếp
=>\(\widehat{AKM}=\widehat{ACM}=45^0\)
Xét ΔMHK có \(\widehat{MHK}+\widehat{MKH}=45^0+45^0=90^0\)
nên ΔMHK vuông cân tại M


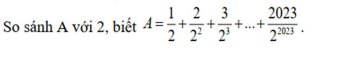
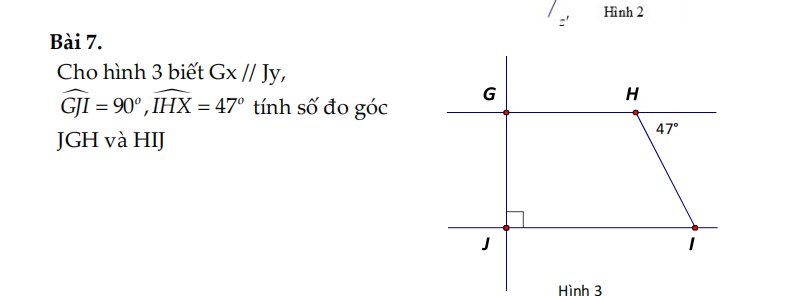
Vì Gx // Jy \(\Rightarrow\left\{{}\begin{matrix}\widehat{JGH}=\widehat{GIJ}=90^{\circ}\left(\text{hai góc đồng vị}\right)\\\widehat{HIJ}=\widehat{IHX}=47^{\circ}\left(\text{hai góc so le trong}\right)\end{matrix}\right.\)