Thi rung chuông vàng cần ôn j zợ mn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trước hết ta sẽ chứng minh: \(\dfrac{x^2}{a}+\dfrac{y^2}{b}\ge\dfrac{\left(x+y\right)^2}{a+b}\)(1)
Ta có (1) tương đương với:
\(x^2b\left(a+b\right)+y^2a\left(a+b\right)\ge\left(x+y\right)^2ab\)
\(\Leftrightarrow\left(xb-ya\right)^2\ge0\) (luôn đúng)
Dấu \(=\) xảy ra khi \(xb=ya\Leftrightarrow\dfrac{x}{a}=\dfrac{y}{b}\).
Áp dụng bất đẳng thức (1) ta có:
\(\dfrac{x^2}{a}+\dfrac{y^2}{b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y\right)^2}{a+b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y+z\right)^2}{a+b+c}\)
Dấu \(=\) xảy ra khi \(\dfrac{x}{a}=\dfrac{b}{y}=\dfrac{z}{c}\).

\(P=\left(\dfrac{a^2+2a}{a^3+2a^3+4a+8}+\dfrac{2}{a^2+4}\right)\div\dfrac{a^3-4a}{a^3-2a^2+4a-8}\)
\(=\left[\dfrac{a\left(a+2\right)}{\left(a+2\right)\left(a^2+4\right)}+\dfrac{2}{a^2+4}\right].\dfrac{\left(a-2\right)\left(a^2+4\right)}{a\left(a^2-4\right)}\)
\(=\dfrac{a+2}{a^2+4}.\dfrac{\left(a-2\right)\left(a^2+4\right)}{a.\left(a-2\right)\left(a+2\right)}=\dfrac{1}{a}\)

\(\dfrac{x^2+1}{3x-13}\)<0
\(\Leftrightarrow\)x\(^2\)+1<0
\(\Leftrightarrow\)x\(^2\)<-1 (vô lí)
Vậy bất phương trình vô nghiệm
\(\dfrac{x^2+1}{3x-13}\)<0 ( x khác 13/3)
mà x2+1>0
=> 3x-13 <0
=> x<13/3
 các bạn giải chi tiết giúp mik nhé
các bạn giải chi tiết giúp mik nhé


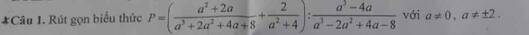
ghê vậy mik ko bt chưa xem rung chuông vàng bao h nói j đến thi chắc là bn xem lại mấy mùa trc của rung chuông vàng ấy rồi học
Lên mạng tra nha bạn, xem cả phần thi mấy mùa trước nữa