tìm stn x biết (x-1/3)^2-1/16=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
Mẫu số chung 2 phân số: 63
\(\dfrac{-3}{7}=\dfrac{-3\cdot9}{7\cdot9}=\dfrac{-27}{63}\)
\(\dfrac{-4}{9}=\dfrac{-4\cdot7}{9\cdot7}=\dfrac{-28}{63}\)
Vì \(-27>-28\) nên\(\dfrac{-27}{63}>\dfrac{-28}{63}\)
Vậy \(\dfrac{-3}{7}>\dfrac{-4}{9}\)
b)
\(\dfrac{10}{15}=\dfrac{10:5}{15:5}=\dfrac{2}{3}\)
\(\dfrac{12}{16}=\dfrac{12:4}{16:4}=\dfrac{3}{4}\)
\(\dfrac{2}{3}=1-\dfrac{1}{3}\)
\(\dfrac{3}{4}=1-\dfrac{1}{4}\)
\(\Rightarrow\dfrac{3}{4}>\dfrac{2}{3}\)
c)
\(\dfrac{99}{-98}< 0< \dfrac{33}{49}\Rightarrow\dfrac{99}{98}< \dfrac{33}{49}\)
d) \(\dfrac{105}{106}< 1< \dfrac{94}{93}\Rightarrow\dfrac{105}{106}< \dfrac{94}{93}\)
e)
\(\dfrac{63}{64}=1-\dfrac{1}{64}\)
\(\dfrac{32}{33}=1-\dfrac{1}{33}\)
Vì \(64>33\) nên \(\dfrac{1}{64}< \dfrac{1}{33}\)
\(\Rightarrow1-\dfrac{1}{64}>1-\dfrac{1}{33}\)
Vậy \(\dfrac{63}{64}>\dfrac{32}{33}\)
f)
\(\dfrac{2020}{2019}=1+\dfrac{1}{2019}\)
\(\dfrac{2022}{2021}=1+\dfrac{1}{2021}\)
Vì \(2019< 2021\) nên \(\dfrac{2020}{2019}>\dfrac{2022}{2021}\)
\(\Rightarrow1+\dfrac{1}{2019}>1+\dfrac{1}{2021}\)
Vậy \(\dfrac{2020}{2019}>\dfrac{2022}{2021}\)

A = \(\dfrac{1}{3}-\dfrac{2}{3^2}+\dfrac{3}{3^3}-\dfrac{4}{3^4}+...+\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}\)
3A = 1 - \(\dfrac{2}{3^{ }}\) + \(\dfrac{3}{3^2}\) - \(\dfrac{4}{3^3}\) + ... + \(\dfrac{99}{3^{98}}\) - \(\dfrac{100}{3^{99}}\)
3A+A = 1-\(\dfrac{2}{3^{ }}\)+\(\dfrac{3}{3^2}\)-\(\dfrac{4}{3^3}\)+...+\(\dfrac{99}{3^{98}}\)-\(\dfrac{100}{3^{99}}\)+\(\dfrac{1}{3}-\dfrac{2}{3^2}+...+\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}\)
4A = 1-(\(\dfrac{2}{3}\)-\(\dfrac{1}{3}\)) +(\(\dfrac{3}{3^2}\)-\(\dfrac{2}{3^2}\))-(\(\dfrac{4}{3^3}\)-\(\dfrac{3}{3^3}\))+...+(\(\dfrac{99}{3^{98}}\)-\(\dfrac{98}{3^{98}}\))-(\(\dfrac{100}{3^{99}}\)-\(\dfrac{99}{3^{99}}\))-\(\dfrac{100}{3^{100}}\)
4A = 1-\(\dfrac{1}{3}\)+\(\dfrac{1}{3^2}\)-\(\dfrac{1}{3^3}\)+...+\(\dfrac{1}{3^{98}}\)-\(\dfrac{1}{3^{99}}\)-\(\dfrac{100}{3^{100}}\)
12A = 3-1+\(\dfrac{1}{3}\)-\(\dfrac{1}{3^2}\)+....+\(\dfrac{1}{3^{97}}\)-\(\dfrac{1}{3^{98}}\)-\(\dfrac{100}{3^{99}}\)
12A+4A=3-1+\(\dfrac{1}{3}\)-\(\dfrac{1}{3^2}\)+..+\(\dfrac{1}{3^{97}}\)-\(\dfrac{1}{3^{98}}\)-\(\dfrac{100}{3^{99}}\)+1-\(\dfrac{1}{3}\)+\(\dfrac{1}{3^2}\)-\(\dfrac{1}{3^3}\)+..+\(\dfrac{1}{3^{98}}\)-\(\dfrac{1}{3^{99}}\)-\(\dfrac{100}{3^{100}}\)
16A = 3+(-1+1)+(\(\dfrac{1}{3}-\dfrac{1}{3}\))+...+(-\(\dfrac{1}{3^{98}}\)+\(\dfrac{1}{3^{98}}\))+(-\(\dfrac{100}{3^{99}}\)-\(\dfrac{1}{3^{99}}\)) - \(\dfrac{100}{3^{100}}\)
16A = 3 - \(\dfrac{101}{3^{99}}\) - \(\dfrac{100}{3^{100}}\)
16A = 3 - \(\dfrac{303}{3^{100}}\) - \(\dfrac{100}{3^{100}}\)
16A = 3 - \(\dfrac{403}{3^{100}}\)
A = \(\dfrac{3}{16}\) - \(\dfrac{403}{16.3^{100}}\) < \(\dfrac{3}{16}\) < \(\dfrac{3}{14}\) (đpcm)

\(a,\dfrac{7}{-9}+\dfrac{-1}{-9}=\dfrac{-7}{9}+\dfrac{1}{9}=\dfrac{-7+1}{9}=\dfrac{-6}{9}=\dfrac{-2}{3}\\ b,\dfrac{7}{-18}+\left(\dfrac{-5}{12}-\dfrac{13}{-18}\right)=\dfrac{-7}{18}-\dfrac{5}{12}+\dfrac{13}{18}=\left(\dfrac{13}{18}-\dfrac{7}{18}\right)-\dfrac{5}{12}\\ =\dfrac{6}{18}-\dfrac{5}{12}=\dfrac{1}{3}-\dfrac{5}{12}=\dfrac{1.4-5}{12}=\dfrac{-1}{12}\\ c,5-\dfrac{-7}{8}+\dfrac{15}{-20}=5+\dfrac{7}{8}-\dfrac{3}{4}=\dfrac{5.8+7-3.2}{8}=\dfrac{40+7-6}{8}=\dfrac{41}{8}\)
a) \(\dfrac{7}{-9}+\dfrac{-1}{-9}=\dfrac{6}{-9}=\dfrac{-2}{3}\)
b) \(\dfrac{7}{-18}+\left(\dfrac{-5}{12}-\dfrac{13}{-18}\right)\)
\(=\dfrac{7}{-18}-\dfrac{5}{12}-\dfrac{13}{-18}\)
\(=\dfrac{-6}{-18}-\dfrac{5}{12}\)
\(=\dfrac{1}{3}-\dfrac{5}{12}=\dfrac{4}{12}-\dfrac{5}{12}\)
\(=\dfrac{-1}{12}\)
c) \(5-\dfrac{-7}{8}+\dfrac{15}{20}\)
\(=5-\dfrac{-7}{8}+\dfrac{3}{4}\)
\(=5-\dfrac{-7}{8}+\dfrac{6}{8}\)
\(=5-\dfrac{-1}{8}=5+\dfrac{1}{8}\)
\(=\dfrac{41}{8}\)

1; (\(\dfrac{-4}{25}\)).(-\(\dfrac{-25}{8}\))
= \(\dfrac{-4.25}{25.4.2}\)
= \(-\dfrac{1}{2}\)
2; \(\dfrac{5}{-14}\).(\(\dfrac{-7}{10}\))
= \(\dfrac{5.\left(-7\right)}{2.5.\left(-7\right).2}\)
= \(\dfrac{1}{4}\)
3; \(\dfrac{-15}{4}\).(\(\dfrac{-16}{25}\))
= \(\dfrac{3.5.4.4}{4.5.5}\)
= \(\dfrac{12}{5}\)
4; 15. (- \(\dfrac{13}{10}\))
= 5.3.\(\dfrac{\left(-13\right)}{2.5}\)
= - \(\dfrac{39}{2}\)

\(D=\left\{6;7;8;9;10;11\right\}\)
\(D=\left\{x|x\in N,5< x< 12\right\}\)
____
\(5\notin D\)
\(7\in D\)
\(17\notin D\)
\(0\notin D\)
\(10\in D\)

Bài 1:
a; A = \(\dfrac{n-7}{n-4}\) (n \(\in\) Z)
A là phân số ⇔ n \(\in\) Z; n - 4 ≠ 0 ⇒ n ≠ 4
Vậy A là phân số khi 4 ≠ n \(\in\) Z
b; A \(\in\) Z ⇔ n - 7 ⋮ n - 4
n - 4 - 3 ⋮ n - 4
3 ⋮ n - 4
n - 4 \(\in\) Ư(3) = {-3; -1; 1; 3}
Lập bảng ta có:
| n-4 | -3 | -1 | 1 | 3 |
| n | 1 | 3 | 5 | 7 |
Theo bảng trên ta có n \(\in\) {1; 3; 5; 7}
Vậy n \(\in\) {1; 3; 5; 7}
Bài 2:
1; \(\dfrac{2009.2010-1}{2009.2010}\)
= \(\dfrac{2009.2010}{2009.2010}-\dfrac{1}{2009.2010}\)
= 1 - \(\dfrac{1}{2009.2010}\)
\(\dfrac{2010.2011-1}{2010.2011}\)
= \(\dfrac{2010.2011}{2010.2011}-\dfrac{1}{2010.2011}\)
= 1 - \(\dfrac{1}{2010.2011}\)
Vì \(\dfrac{1}{2009.2010}>\dfrac{1}{2010.2011}\)
Vậy \(\dfrac{2009.2010-1}{2009.2010}< \dfrac{2010.2011-1}{2010.2011}\)

a, A={8;9;10;11;12;13;14}
b, Các số 10;13 là các phần tử thuộc A. Các số 16;19 không phải phần tử thuộc A
c, B={8;10;12;14}
\(B=\left\{x\in N|x=2n;n\in N;3< n< 8\right\}\)
a)
\(A=\left\{x\in N\text{|}7< x< 15\right\}\)
b) Loại các số không lớn hơn 7: không loại số nào
Loại các số không nhỏ hơn 15: 16 và 19
Vậy các số thuộc tập A là 10 và 13
Các số không thuộc tập A là 16 và 19
c)
\(B=\left\{8;10;12;14\right\}\)
\(B=\left\{x\in N\text{|}x⋮2,8\le x\le14\right\}\)

Thực hành 2
a) \(E=\left\{x\in N\text{|}x⋮2,0\le x\le8\right\}\)
b) \(P=\left\{11;12;13;14;15;16;17;18;19\right\}\)

Ta thấy \(p^2+2q=10\)
\(\Rightarrow p\) chẵn \(\Rightarrow p=2\) \(\Rightarrow2^2+2q=10\) \(\Rightarrow q=3\), nhận.
Vậy \(\left(p,q\right)=\left(2,3\right)\)
À bài đó mình nhầm đề. Bài này phải làm như sau:
Ta thấy \(p^2+2q=10\)
\(\Leftrightarrow q=\dfrac{10-p^2}{2}\) \(\Rightarrow p\) chẵn
Có thế thấy nếu ta thay bất kì \(p\) chẵn nào thì đều tìm được \(q\) thỏa mãn. Chẳng hạn:
\(\left(p,q\right)\in\left\{\left(0,5\right),\left(\pm2,3\right),\left(\pm4,-3\right),\left(\pm6,-13\right),...\right\}\)
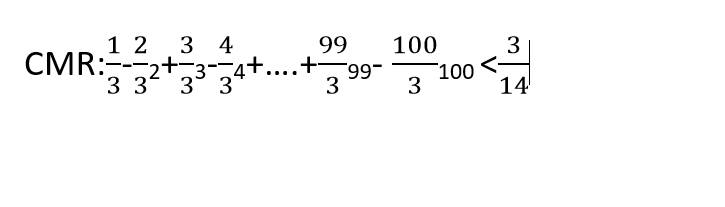
\(\left(x-\dfrac{1}{3}\right)^2-\dfrac{1}{16}=0\)
\(\left(x-\dfrac{1}{3}\right)^2=\dfrac{1}{16}\)
\(\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{1}{4}\\x-\dfrac{1}{3}=-\dfrac{1}{4}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{7}{12}\\x=\dfrac{1}{12}\end{matrix}\right.\)