Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 60 sản phẩm. Khi thực hiện do cải tiến kĩ thuật nên mỗi ngày tổ đã sản xuất tăng thêm được 5 sản phẩm. Do đó tổ đã hoàn thành trước kế hoạch 2 ngày và còn vượt mức 15 sản phẩm.Hỏi theo kế hoạch, tổ phải sản xuất bao nhiêu sản phẩm?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét tam giác ABC và tam giác HBA có
^ABC _ chung
^BAC = ^BHA = 900
Vậy tam giác ABC ~ tam giác HBA (g.g)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
c, Chu vi tam giác ABC là
10 + 6 + 8 = 24 cm
d, Ta có \(\dfrac{AB}{HB}=\dfrac{BC}{AB}\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)
Lại có \(\dfrac{AC}{AH}=\dfrac{BC}{AB}\Rightarrow AH=\dfrac{AC.AB}{BC}=\dfrac{48}{10}=\dfrac{24}{5}cm\)

Áp dụng bất đẳng thức Cauchy Schwartz, ta được:
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1^2}{a}+\dfrac{2^2}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\)
Áp dụng bất đẳng thức Cauchy Schwartz, ta được:
\(\left(a+2b\right)^2=\left(a.1+\sqrt{2}.\sqrt{2}b\right)^2\le\left(a^2+2b^2\right).3\)
\(\Rightarrow a+2b\le\sqrt{3\left(a^2+2b^2\right)}\le\sqrt{9c^2}=3c\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{2}{b}\ge\dfrac{9}{3c}=\dfrac{3}{c}\)
\(\Rightarrow P\ge\dfrac{3}{c}.c=3\)
Dấu "=" xảy ra khi \(a=b=c=1\)

gọi số tuổi của Phương hiện tại là a (a ϵ N*)
gọi số tuổi của mẹ hiện tại là b (b ϵ N*)
ta có hiện tại tuổi mẹ gấp 3 lần tuổi Phương
→a=3b (1)
ta có 13 năm nữa tuổi mẹ gấp 2 lần tuổi Phương
→a+13=2(b+13)
→a+13=2b+26
→a=2b+13 (2)
từ (1) và (2) suy ra : 3b=2b+13
→b=13
vậy năm nay Phương 13 tuổi

\(\left(3x-1\right)^2-3\left(x-1\right)\left(x+3\right)\)
\(=9x^2-6x+1-3\left(x^2+2x-3\right)\)
\(=9x^2-6x+1-3x^2-6x+9\)
\(=6x^2-12x+10\)
\(=6\left(x^2-2x+\dfrac{10}{6}\right)\)
\(=6\left(x^2-2x.1+1-1+\dfrac{10}{6}\right)\)
\(=6\left[\left(x-1\right)^2+\dfrac{4}{6}\right]\)
\(=6\left(x-1\right)^2+4>0\forall x\inℝ\)
Vậy bất phương trình luôn đúng.

\(9x^2-6x+1-3\left(x^2+2x-3\right)\)
\(=6x^2-12x+10=6\left(x^2-2x+1-1\right)+10\)
\(\Leftrightarrow6\left(x-1\right)^2+4>0\)(luôn đúng)

\(\left(2x-1\right)\left(2x-3\right)\left(x+1\right)^2=18\)
\(\Leftrightarrow\left(2x-1\right)\left(2x-3\right)\left(2x+2\right)^2=72\) (*)
Đặt \(a=2x+2\)
(*) \(\Leftrightarrow\left(a-3\right)\left(a-5\right).a^2=0\)
\(\Leftrightarrow\left(a^3-5a^2\right)\left(a-3\right)=0\)
\(\Leftrightarrow a^4-8a^3+15a^2=0\)
\(\Leftrightarrow a^4-5a^3-3a^3+15a^2=0\)
\(\Leftrightarrow a^3.\left(a-5\right)-3a^2.\left(a-5\right)=0\)
\(\Leftrightarrow\left(a-5\right)\left(a-3\right).a^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\2x-1=0\\\left(2x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)

\(\left(2-3x\right)^2=\dfrac{1}{36}=\left(\dfrac{1}{6}\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}2-3x=\dfrac{1}{6}\\2-3x=-\dfrac{1}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{18}\\x=\dfrac{13}{18}\end{matrix}\right.\)
\(\left[{}\begin{matrix}2-3x=\dfrac{1}{6}\\2-3x=-\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{11}{6}\\3x=\dfrac{13}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{6}:3=\dfrac{11}{18}\\x=\dfrac{13}{6}:3=\dfrac{13}{18}\end{matrix}\right.\)


 giúp mình với ạ :(
giúp mình với ạ :( 
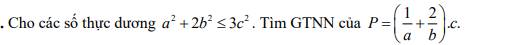
gọi số sản phẩm tổ phải sản xuất theo kế hoạch là : x (x ϵ N*)
→số sản phảm thực tế tổ làm đc là : x+15
theo thực tế thì 1 ngày tổ đó làm đc: 60+5=65(sản phẩm)
ta có, theo thực tế thì tổ đó hoàn thành sản phẩm trước 2 ngày:
→ ta có phương trình
\(\dfrac{x}{60}\)-\(\dfrac{x+15}{65}\)=2
giải hệ phương trình, ta được x=1740(thỏa mãn)