a) \(n+18⋮n+1\)

\(\Rightarrow n+18-\left(n+1\right)⋮n+1\)

\(\Rightarrow n+18-n-1⋮n+1\)

\(\Rightarrow17⋮n+1\)

\(\Rightarrow17⋮n+1\)

\(\Rightarrow n+1\in\left\{-1;1;-17;17\right\}\)

\(\Rightarrow n\in\left\{-2;0;-18;16\right\}\left(n\in Z\right)\)

còn ý b nữa bạn

Ba số nguyên liên tiếp có dạng: n; n + 1; n + 2; với n \(\in\) Z

Tổng ba số nguyên liên tiếp là: A =  n + n + 1 + n + 2 = 3n + 3

A = 3.( n + 1)  

với n là số lẻ ta có: n + 1 là số chẵn ⇒ n + 1 ⋮ 2 ⇒ 3.(n + 1) ⋮ 6

Với n là số chẵn ta có: n + 1 là số lẻ ⇒ n + 1 không chia hết cho 2

Khi đó tổng ba số tự nhiên liên tiếp không chia hết cho 6.

Từ những lập luận trên ta có tổng của ba số nguyên liên tiếp không phải lúc nào cũng chia hết cho 6.

Kết luận việc chứng minh tổng ba số nguyên liên tiếp bất kỳ luôn chia hết cho 6 là điều không thể xảy ra. 

a) 400 - 5x = 200

5x = 200

x = 40

b) 250 : x + 10 = 20

250 : x = 10

x = 25

c) 96 - 3 ( x + 8 ) = 42

3 ( x + 8 ) = 54

( x + 8 ) = 54 : 3

x + 8 = 18

x = 18 - 8

x = 10

d) 36 : ( x - 5 ) = 2²

36 : ( x - 5 ) = 4 

x - 5 = 36 : 4

x - 5 = 9

x = 9 + 5 

x = 14

e) 15 x 5 ( x - 35 ) - 525 = 0

75 ( x - 35 ) - 525 = 0

75 ( x - 35 ) = 525

x - 35 = 7 

x = 7 + 35

x = 42

f) [ 3 x ( 70 - x ) + 5 ] : 2 = 46

[ 3 x ( 70 - x ) + 5 ] = 92

3 x ( 70 - x ) = 87

70 - x = 87 : 3

70 - x = 29 

x = 41

`@` `\text {Ans}`

`\downarrow`

`7,`

Ta có:

`2023 = 2024 - 1`

Mà `x = 2024`

`=> 2023 = x - 1`

Thay `2023 = x - 1` vào `f(x)`

`f(x) =`\(x^{15}-\left(x-1\right)x^{14}-\left(x-1\right)x^{13}-...\left(x-1\right)x^2-\left(x-1\right)x-\left(x-1\right)\)

`=`\(x^{15}-x^{15}+x^{14}-x^{14}+x^{13}-...-x^2+x-x+1\)

`=`\(\left(x^{15}-x^{15}\right)+\left(x^{14}-x^{14}\right)+...+\left(x-x\right)+1\)

`= 1`

Vậy, giá trị của `f(x)` khi `x = 2024` là `f(2024) = 1.`

-0.24>-4/5

8¹⁹⁷⁵ = (8⁴)⁴⁹³.8³ = \(\overline{..6}\)⁴⁹³. \(\overline{...2}\) = \(\overline{..2}\)

8^1975=8^1972*8^3

8^1975=(8^4)^493*512

8^1975= ...6^493*512

8^1975=....6*512

=>8^1975=...2 

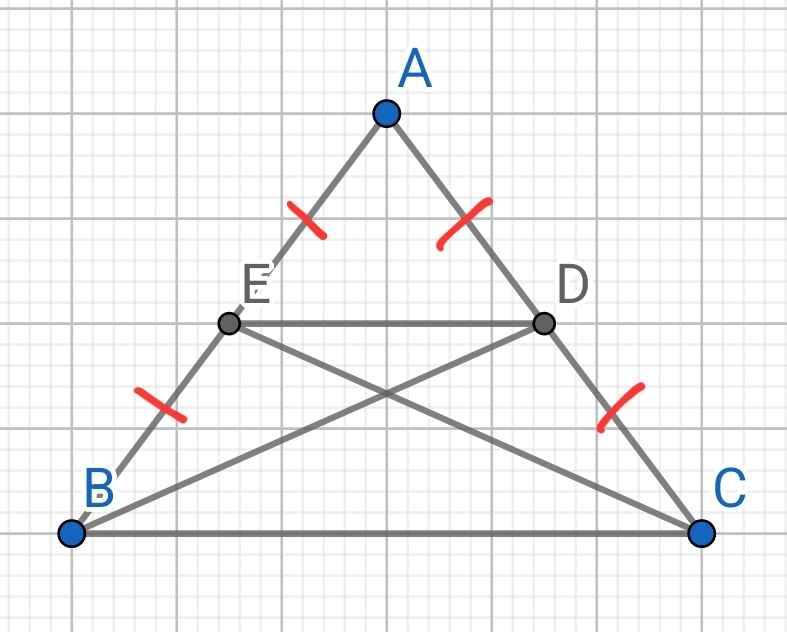
a) Do BD là đường trung tuyến của ∆ABC

⇒ D là trung điểm AC

⇒ AD = AC/2

Do CE là đường trung tuyến của ∆ABC

⇒ E là trung điểm AB

⇒ AE = AB/2

Mà AB = AC (∆ABC cân tại A)

⇒ AD = AC/2 = AB/2 = AE

⇒ ∆ADE cân tại A

b) Do ∆ADE cân tại A (cmt)

⇒ ∠AED = ∠ADE = (180⁰ - ∠BAC)/2

Do ∆ABC cân tại A (gt)

⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC)/2

⇒ ∠AED = ∠ABC = (180⁰ - ∠BAC)/2

Mà ∠AED và ∠ABC là hai góc đồng vị

⇒ ED // BC

∆ABC cân tại A

⇒ ∠ABC = ∠ACB (hai góc ở đáy)

⇒ ∠EBC = ∠DCB

Tứ giác BCDE có:

ED // BC (cmt)

⇒ BCDE là hình thang

Mà ∠EBC = ∠DCB (cmt)

⇒ BCDE là hình thang cân