bn hểu ko

`#040911`

a)

Ta có:

\(\left\{{}\begin{matrix}\text{AB = AC (tg ABC cân tại A)}\\\text{BD = CE (gt)}\end{matrix}\right.\)

`\Rightarrow \text {AD = AE}`

Xét `\Delta ADE:`

`AD = AE`

`\Rightarrow Delta ADE` cân tại A

`\Rightarrow`\(\widehat{\text{ADE}}=\widehat{\text{AED}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`

`\Delta ABC` cân tại A

`\Rightarrow`\(\widehat{\text{ABC}}=\widehat{\text{ACB}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`

Từ `(1)` và `(2)`

`\Rightarrow`\(\widehat{\text{ABC}}=\widehat{\text{ADE}}\)

Mà `2` góc này nằm ở vị trí đồng vị

`\Rightarrow \text {DE // BC (t/c 2 dt' //)}`

b)

Ta có:

\(\widehat{ABC}=\widehat{ACB}\text{ }\left(\Delta ABC\text{ cân tại A}\right)\)

Mà \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{MBD}\text{ }\left(\text{đối đỉnh}\right)\\\widehat{ACB}=\widehat{NCE}\text{ }\left(\text{đối đỉnh}\right)\end{matrix}\right.\) 

`\Rightarrow`\(\widehat{\text{MBD}}=\widehat{\text{NCE}}\)

Xét `\Delta MBD` và `\Delta NCE:`

\(\widehat{\text{BMD}}=\widehat{\text{CNE}}\left(=90^0\right)\)

\(\text{BD = CE (gt)}\)

\(\widehat{\text{MBD}}=\widehat{\text{NCE}}\text{ (CMT)}\)

`\Rightarrow Delta MBD = \Delta NCE (ch - gn)`

`\Rightarrow \text {DM = EN (2 cạnh tương ứng)}`

c)

Vì `\Delta MBD = \Delta NCE (b)`

`\Rightarrow \text {BM = CN (2 cạnh tương ứng)}`

Ta có:

\(\left\{{}\begin{matrix}\widehat{\text{ABM}}+\widehat{\text{ABC}}=180^0\text{ (kề bù)}\\\widehat{\text{ACN}}+\widehat{\text{ACB}}=180^0\text{ (kề bù)}\end{matrix}\right.\)

Mà \(\widehat{\text{ABC}}=\widehat{\text{ACB}}\) `(\Delta ABC` cân tại A`)`

`\Rightarrow`\(\widehat{\text{ABM}}=\widehat{\text{ACN}}\)

Xét `\Delta AMB` và `\Delta ANC:`

\( \text{AB = AC }\left(\Delta\text{ABC cân tại A}\right)\\ \widehat{\text{ABM}}=\widehat{\text{ACN}}\\ \text{BM = CN (CMT)}\)

`\Rightarrow \Delta AMB = \Delta ANC (c-g-c)`

`\Rightarrow \text {AM = AN (2 cạnh tương ứng)}`

Xét `\Delta AMN`

`\text {AM = AN}`

`\Rightarrow \Delta AMN` là `\Delta` cân.

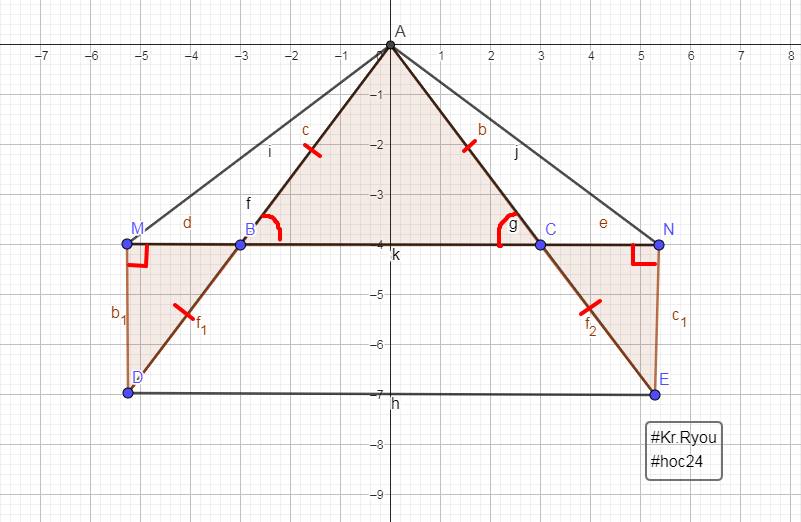
bn ơi mình thấy câu b kẻ thêm nó cứ sao ý

bn có chép đúng đề bài ko

Lời giải:

Do tam giác $ABC=MNP$ nên:

$AB=NM=2$ (cm) 

Chu vi tam giác $MNP$ là:
$MN+NP+MP = 2+4+5=11$ (cm)

Do 2 tam giác bằng nhau nên chu vi tam giác $ABC$ cũng bằng $11$ cm.

4^-1-5\(x\) = 16²

4^-1-5\(x\) = 4⁴

   -1-5\(x\) = 4

        5\(x\) = - 5

           \(x\) = -1

2^3x+1 = 32² 

2^3x+1 = (2⁵)²

2^3x+1 = 2¹⁰

  3x+1= 10 

 3x      = 10 -1 

 3x     = 9

 x = 9:3

x = 3

\(\dfrac{105}{-15}\)  = -7 > - 7,112

Vậy \(\dfrac{105}{-15}\) > -7,112 

105/-15 va -7,112

Ta co : 105/-15 = -7

Ma -7 < -7,112

Vay 105/-15 <-7,112

Góc trong cùng phía với góc MBZ  là góc xAB 

⇒ \(\widehat{xAB}\) + \(\widehat{yAm}\) = 250⁰

mà \(\widehat{xAB}\) = \(\widehat{yAM}\) (vì hai góc đối đỉnh)

⇒ \(\widehat{xAB}\) = 250⁰ : 2 = 125⁰

\(\widehat{xAB}\) + \(\widehat{yAB}\) = 180⁰  (hai góc kề bù)

\(\widehat{yAB}\) = 180⁰ - 125⁰ = 55⁰