cho hình vuông ABCD cạnh=a, I thuộc AB, DI cắt CB tại K. CMR: 1/(DI^2) +1/(DK^2)+1/a^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=sin^210+sin^220+sin^245+sin^270+sin^280\)
\(A=sin^210+sin^220+sin^245+cos^220+cos^210\)
\(A=\left(sin^210+cos^210\right)+\left(sin^220+cos^220\right)+sin^245\)
\(A=1+1+\left(\dfrac{\sqrt{2}}{2}\right)^2\)
\(A=\dfrac{5}{2}\)

6B.
a) Số tiền người sử dụng phải trả nếu đăng kí gói Internet 6 tháng là:
\(C\left(6\right)=70.6+300=720\) (nghìn đồng)
b) Nếu người sử dụng phải thanh toán số tiền cước phí sử dụng Internet là 930 nghìn đồng thì:
\(C\left(x\right)=930\)
\(\Rightarrow70x+300=930\)
\(\Leftrightarrow70x=630\)
\(\Leftrightarrow x=9\)
Vậy thời hạn sử dụng gói cước Internet của người đó là 9 tháng.
6A.
a) Giá tiền của một chiếc ấm đun nước có bán kính đáy ấm 28cm là:
\(\dfrac{11}{8}.28+150=188,5\) (nghìn đồng)
b) Giá tiền của cô Trinh phải trả là:
\(\left(\dfrac{11}{8}.24+150\right)+\left(\dfrac{11}{8}.32+150\right)=377\) (nghìn đồng)
Vì \(400>377\) nên cô Trinh đã mang đủ tiền để trả.
5B.
Gọi số thùng bánh tổ I, tổ II sản xuất được trong tuần thứ nhất lần lượt là \(x,y\) (thùng bánh; \(x,y\in\mathbb{N}^*;x,y<900\))
Vì trong tuần thứ nhất cả hai tổ sản xuất được 900 thùng bánh nên ta có phương trình: \(x+y=900\) (1)
Số thùng bánh tổ I sản xuất được trong tuần thứ hai là: \(x\left(100\%+25\%\right)=1,25x\) (thùng bánh)
Số thùng bánh tổ II sản xuất được trong tuần thứ hai là: \(95\%y=0,95y\)
Vì sang tuần thứ hai cả hai tổ sản xuất được 975 thùng bánh nên ta có phương trình: \(1,25x+0,95y=975\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}x+y=900\\1,25x+0,95y=975\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=400\left(tm\right)\\y=500\left(tm\right)\end{matrix}\right.\)
Vậy: ...

\(A=sin^210^0+sin^220^0+sin^245^0+sin^270^0+sin^280^0\)
\(=\left(sin^210^0+sin^280^0\right)+\left(sin^220^0+sin^270^0\right)+sin^245^0\)
\(=\left(sin^210^0+cos^210^0\right)+\left(sin^220^0+cos^220^0\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)
\(B=tan20^0\cdot tan35^0\cdot tan45^0\cdot tan55^0\cdot tan20^0\)
\(=tan^220^0\cdot tan35^0\cdot cot35^0\cdot1=tan^220^0\)
\(C=3\cdot\left(sin^4\alpha+cos^4\alpha\right)-2\left(sin^6\alpha+cos^6\alpha\right)\)
\(=3\left[\left(sin^2\alpha+cos^2\alpha\right)^2-2\cdot sin^2\alpha\cdot cos^2\alpha\right]-2\left[\left(sin^2\alpha+cos^2\alpha\right)^3-3\cdot sin^2\alpha\cdot cos^2\alpha\cdot\left(sin^2\alpha+cos^2\alpha\right)\right]\)
\(=3\left[1-2\cdot sin^2\alpha\cdot cos^2\alpha\right]-2\left[1-3\cdot sin^2\alpha\cdot cos^2\alpha\right]\)
\(=3-6\cdot sin^2\alpha\cdot cos^2\alpha-2+6\cdot sin^2\alpha\cdot cos^2\alpha\)
=1
\(D=\sqrt{sin^2\alpha}+4\cdot cos^2\alpha+\sqrt{cos^2\alpha}+4\cdot sin^2\alpha\)
\(=\left|sin\alpha\right|+\left|cos\alpha\right|+4\cdot\left(cos^2\alpha+sin^2\alpha\right)=\left|sin\alpha\right|+\left|cos\alpha\right|+4\)


Gọi T là giao điểm của 2 tiếp tuyến tại A và B của (O). Qua N kẻ đường thẳng song song với AM cắt AB tại C. Gọi I là giao điểm của AB và MN.
Khi đó, theo tính chất của 2 tiếp tuyến cắt nhau, ta có \(TA=TB\) \(\Rightarrow\Delta TAB\) cân tại T \(\Rightarrow\widehat{TBA}=\widehat{TAB}\)
Vì NC//TA nên \(\widehat{NCB}=\widehat{TAB}\) (2 góc đồng vị)
Từ đó \(\Rightarrow\widehat{TBA}=\widehat{NCB}\) \(\Rightarrow\Delta NCB\) cân tại N
\(\Rightarrow NC=NB\)
Mà \(NB=MA\) nên \(NC=MA\)
Do đó tứ giác NAMC là hình bình hành (vì có NC//MA và \(NC=MA\))
\(\Rightarrow\) MN và AC cắt nhau tại trung điểm I của mỗi đoạn
\(\Rightarrow\) I là trung điểm MN
\(\Rightarrow\) AB chia đôi MN (đpcm)

\(\dfrac{2\left(1-3x\right)}{5}-2+\dfrac{3x}{10}=8-\dfrac{2x+1}{4}\)
\(\Leftrightarrow\dfrac{8\left(1-3x\right)}{20}-\dfrac{40}{20}+\dfrac{6x}{20}=\dfrac{160}{20}-\dfrac{5\left(2x+1\right)}{20}\)
\(\Leftrightarrow8\left(1-3x\right)-40+6x=160-5\left(2x+1\right)\)
\(\Leftrightarrow8-24x-40+6x=160-10x-5\)
\(\Leftrightarrow-18x-32=155-10x\)
\(\Leftrightarrow-18x+10x=155+32\)
\(\Leftrightarrow-8x=187\)
\(\Leftrightarrow x=-\dfrac{187}{8}\)
Vậy: ...

l: \(L=\sqrt{4\sqrt{6}+8\sqrt{3}+4\sqrt{2}+18}\)
\(=\sqrt{12+4+2+2\cdot2\sqrt{3}\cdot2+2\cdot2\sqrt{3}\cdot\sqrt{2}+2\cdot2\cdot\sqrt{2}}\)
\(=\sqrt{\left(2\sqrt{3}+\sqrt{2}+2\right)^2}=2\sqrt{3}+\sqrt{2}+2\)
m: \(M=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+10\sqrt{7-4\sqrt{3}}}}}\)
\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+10\sqrt{\left(2-\sqrt{3}\right)^2}}}}\)
\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+10\left(2-\sqrt{3}\right)}}}\)
\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{8+20-10\sqrt{3}}}}\)
\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)
\(=\sqrt{9-\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)
\(=\sqrt{9-\sqrt{5\sqrt{3}+5\left(5-\sqrt{3}\right)}}\)
\(=\sqrt{9-\sqrt{5\sqrt{3}+25-5\sqrt{3}}}=\sqrt{9-\sqrt{25}}=\sqrt{4}=2\)
p: \(P=\sqrt{14+\sqrt{40}+\sqrt{56}+\sqrt{140}}\)
\(=\sqrt{14+2\cdot\sqrt{2}\cdot\sqrt{5}+2\cdot\sqrt{2}\cdot\sqrt{7}+2\cdot\sqrt{5}\cdot\sqrt{7}}\)
\(=\sqrt{5+2+7+2\cdot\sqrt{2}\cdot\sqrt{5}+2\cdot\sqrt{2}\cdot\sqrt{7}+2\cdot\sqrt{5}\cdot\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{2}+\sqrt{5}+\sqrt{7}\right)^2}=\sqrt{2}+\sqrt{5}+\sqrt{7}\)

b: \(cos14=sin76;cos37=sin53\)
Vì 47<48<53<76 nên \(sin47< sin48< sin53< sin76\)
=>\(sin47< sin48< cos37< cos14\)
c: \(cot25=tan65;cot38=tan52\)
Vì 52<62<65<73
nên \(tan52< tan62< tan65< tan73\)
=>\(cot38< tan63< cot25< tan73\)
a: Vì 75>45
nên \(tan75>1\)
Vì 40<45
nên \(cot40>1\)
\(cot40=tan50;tan75=tan75\)
mà \(tan50< tan75\)
nên \(1< cot40< tan75\left(1\right)\)
\(cos56=sin34;sin50=sin50\)
mà 34<50
nên \(sin34< sin50< 1\)
=>\(cos56< sin50< 1\left(2\right)\)
Từ (1),(2) suy ra \(cos56< sin50< cot40< tan75\)

Xét ΔABC vuông tại A có \(\widehat{B}+\widehat{C}=90^0\)
nên \(sinB=cosC=\dfrac{4}{5}\)
\(sin^2B+cos^2B=1\)
=>\(cos^2B=1-\left(\dfrac{4}{5}\right)^2=\dfrac{9}{25}=\left(\dfrac{3}{5}\right)^2\)
=>\(cosB=\dfrac{3}{5}\)
\(tanB=\dfrac{sinB}{cosB}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotB=\dfrac{1}{tanB}=\dfrac{3}{4}\)
Vì tam giác ABC vuông tại A
Nên: \(\widehat{B}+\widehat{C}=90^o\\ \Rightarrow0^o< \widehat{C}< 90^o\)
\(\Rightarrow0< \sin C< 1\)
Ta có: \(\sin^2C+\cos^2C=1\Rightarrow\sin^2C=1-\left(\dfrac{4}{5}\right)^2=\dfrac{9}{25}\\ \Rightarrow\sin C=\dfrac{3}{5}\)
Lại có: \(\tan C=\dfrac{\sin C}{\cos C}=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}\\ \cot C=\dfrac{1}{\tan C}=\dfrac{4}{3}\)

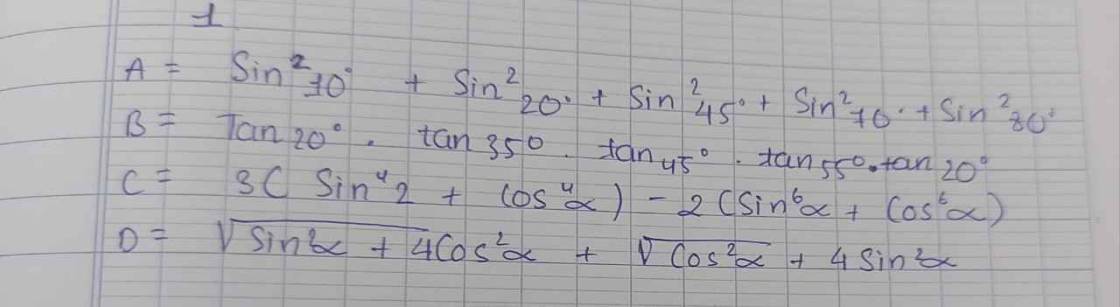

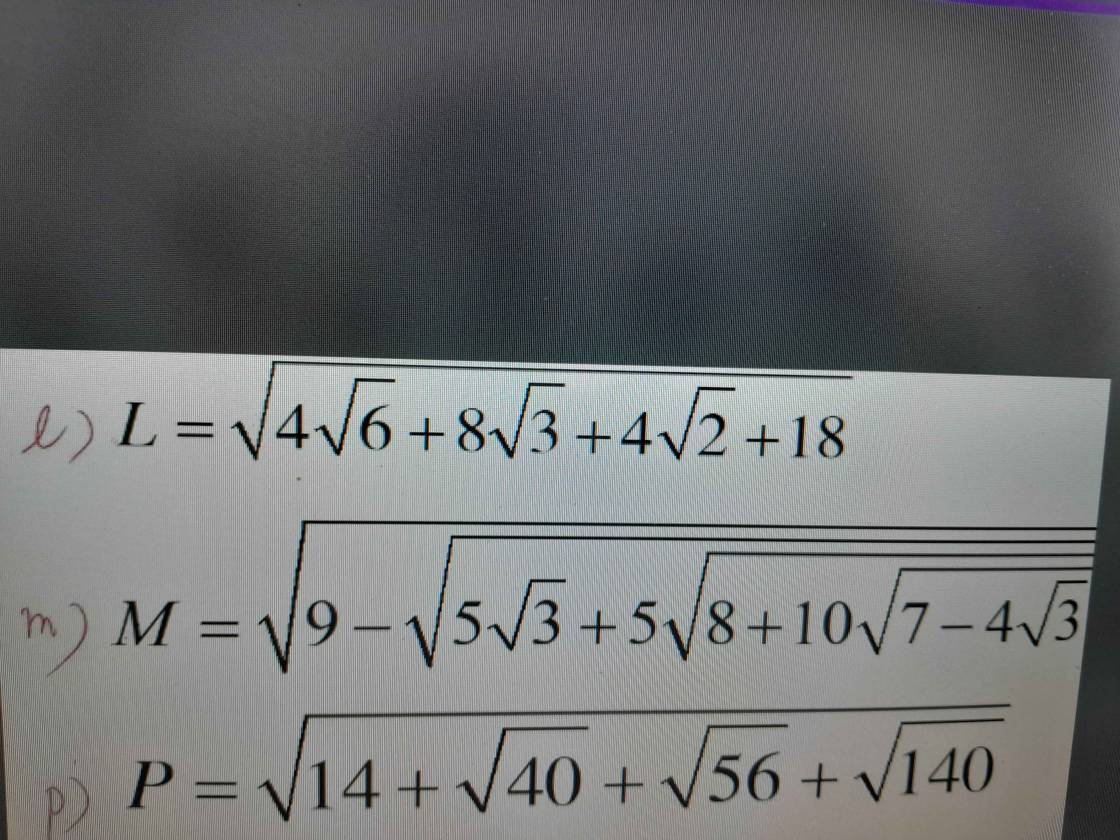

Sửa lại đề bài là cm \(\dfrac{1}{DI^2}+\dfrac{1}{DK^2}=\dfrac{1}{a^2}\) nhé.
Qua D kẻ đường thẳng vuông góc với DE cắt BC tại F.
Khi đó \(\widehat{DAI}=\widehat{CDF}\) (vì cùng phụ với \(\widehat{IDC}\))
Tứ giác ABCD là hình vuông nên \(DA=DC\)
Xét tam giác ADI và CDF, ta có:
\(\widehat{DAI}=\widehat{DCF}=90^o;DA=DC;\widehat{ADI}=\widehat{CDF}\)
\(\Rightarrow\Delta ADI=\Delta CDF\left(g.c.g\right)\)
\(\Rightarrow DI=DF\)
Tam giác DKF vuông tại D có đường cao DC \(\left(C\in KF\right)\) nên:
\(\dfrac{1}{DF^2}+\dfrac{1}{DK^2}=\dfrac{1}{DC^2}\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{DI^2}+\dfrac{1}{DK^2}=\dfrac{1}{a^2}\) (do \(DI=DF,DC=a\))
Ta có đpcm.