Bức tranh Tuyên ngôn độc lập tả cảnh Ủy ban Năm trình bày kế hoạch giành độc lập cho Quốc hội vào ngày 28 tháng 6 năm 1776

 Sửa đề:

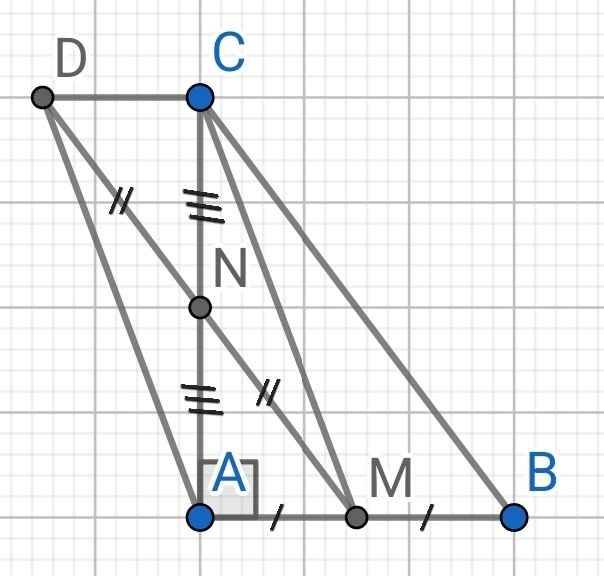
a) Chứng minh tứ giác BMDC là hình bình hành

b) Tứ giác AMCD là hình gì? Vì sao?

GIẢI

a) Do M là trung điểm AB

N là trung điểm AC

⇒ MN là đường trung bình của ∆ABC

⇒ MN // BC và MN = BC : 2

Do MN // BC (cmt)

⇒ MD // BC

Ta có:

ND = NM (gt)

⇒ MN = MD : 2

Mà MN = BC : 2 (cmt)

⇒ MD = BC

Tứ giác BMDC có:

MD // BC (cmt)

MD = BC (cmt)

⇒ BMDC là hình bình hành

b) Do BMDC là hình bình hành (cmt)

⇒ BM // CD và BM = CD

⇒ AM // CD

Lại có:

M là trung điểm của AB (gt)

⇒ AM = BM = AB : 2

Mà BM = CD (cmt)

⇒ AM = CD

Tứ giác AMCD có:

AM // CD (cmt)

AM = CD (cmt)

⇒ AMCD là hình bình hành

Khí helium (He) có một số tính chất đặc biệt làm cho nó được sử dụng trong các ứng dụng như bơm khinh khí cầu hoặc bóng thám không:

1. Tính nhẹ: Khí helium có khối lượng riêng rất nhẹ, chỉ bằng khoảng 1/7 so với không khí. Điều này làm cho nó trở thành một lựa chọn lý tưởng để tạo ra sự nâng đỡ và đẩy lên cho các khinh khí cầu hoặc bóng thám không.

2. Không cháy: Helium là một khí không cháy, không gây cháy nổ. Điều này làm cho nó an toàn khi sử dụng trong các ứng dụng không gian hẹp như bóng thám không, nơi mà sự an toàn là yếu tố quan trọng.

3. Không gây độc: Helium là một khí không màu, không mùi và không gây độc hại cho con người. Điều này làm cho nó an toàn khi được sử dụng trong môi trường sống và làm việc.

4. Dễ dàng tìm kiếm: Helium là một nguyên tố phổ biến trong tự nhiên và có thể được tìm thấy trong khí quyển. Điều này làm cho nó dễ dàng tiếp cận và sử dụng trong các ứng dụng thực tế.

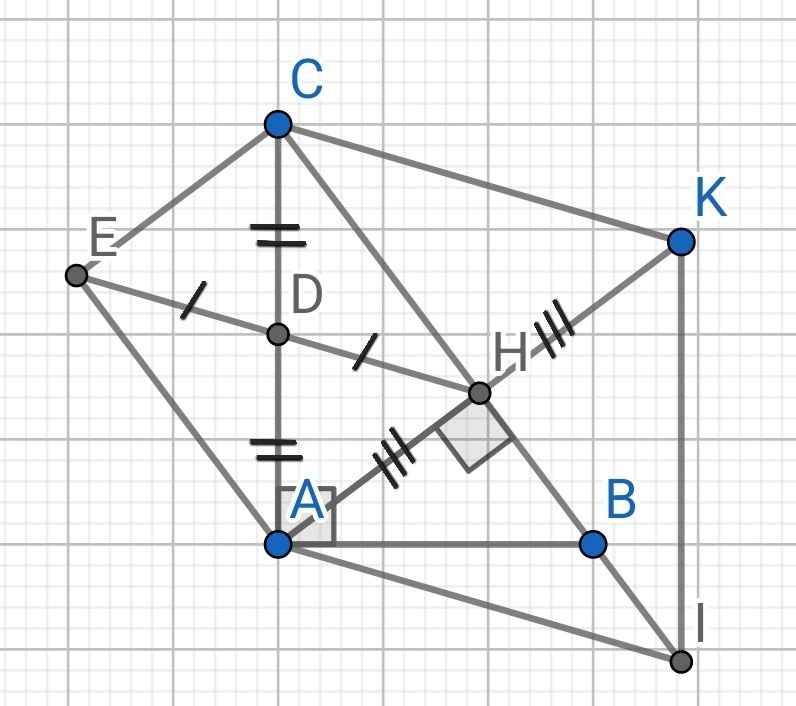a) Do AH là đường cao của ∆ABC

⇒ AH ⊥ BC

⇒ ∠AHC = 90⁰

Tứ giác AHCE có:

D là trung điểm AC (gt)

D là trung điểm HE (gt)

⇒ AHCE là hình bình hành

Mà ∠AHC = 90⁰ (cmt)

⇒ AHCE là hình chữ nhật

b) Do AHCE là hình chữ nhật (cmt)

⇒ AE // HC

⇒ AE // HI

Tứ giác AEIH có:

AE // HI (cmt)

AI // HE (gt)

⇒ AEIH là hình bình hành

c) Do AHCE là hình chữ nhật (cmt)

⇒ AC = HE

Do AEIH là hình bình hành (cmt)

⇒ HE = AI

⇒ AC = AI

⇒ ∆ACI cân tại A

Lại có:

AH ⊥ BC (cmt)

⇒ AH ⊥ CI

AH là đường cao của ∆ACI

⇒ AH cũng là đường trung tuyến của ∆ACI

⇒ H là trung điểm của CI

Do HA = HK (gt)

⇒ H là trung điểm của AK

Do AH ⊥ CI (cmt)

⇒ AH ⊥ CK

Tứ giác ACKI có:

H là trung điểm CI (cmt)

H là trung điểm của AK (cmt)

⇒ ACKI là hình bình hành

Mà AK ⊥ CI (cmt)

⇒ ACKI là hình thoi

⇒ AK là tia phân giác của ∠IAC

d) Để CAIK là hình vuông thì AC ⊥ AI

Mà AC ⊥ AB và AC = AI

⇒ AC = AB (B ≡ I)

⇒ ∆ABC vuông cân tại A

⇒ AH vừa là đường cao, vừa là đường trung tuyến của ∆ABC

⇒ AH = HC = BC : 2

Mà tứ giác AHCE là hình chữ nhật có AH = HC

⇒ AHCE là hình vuông

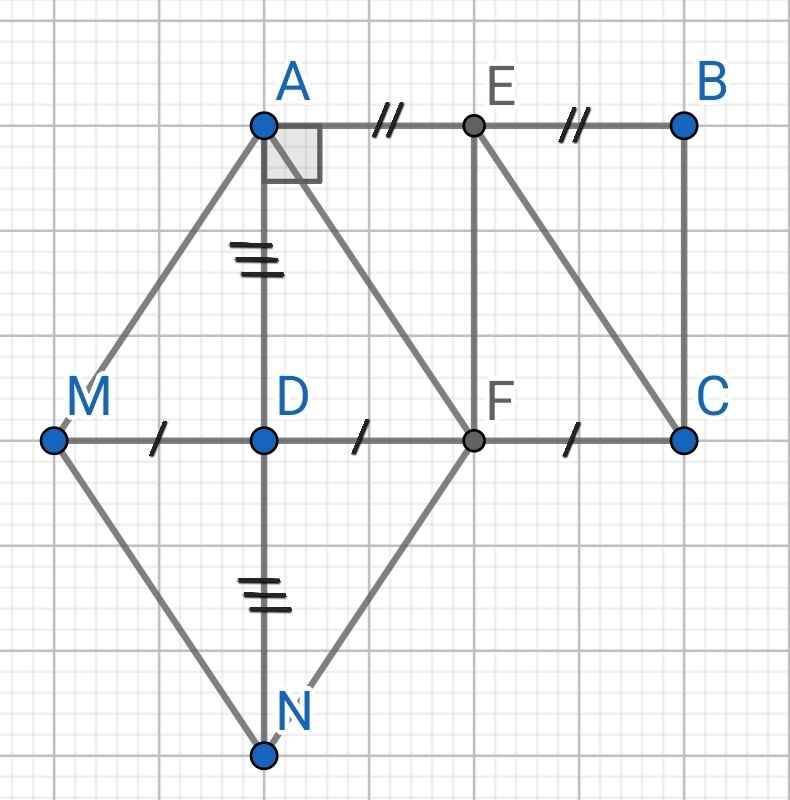 a) Do ABCD là hình chữ nhật (gt)

⇒ AB = CD (1)

Do E là trung điểm của AB

⇒ AE = BE = AB : 2 (2)

Do F là trung điểm của CD (gt)

⇒ CF = DF = CD : 2 (3)

Từ (1), (2) và (3) ⇒ AE = CF

Do ABCD là hình chữ nhật (gt)

⇒ AB // CD

⇒ AE // CF

Tứ giác AECF có:

AE // CF (cmt)

AE = CF (cmt)

⇒ AECF là hình bình hành

b) Do AE = CF (cmt)

CF = DF (cmt)

⇒ AE = DF

Do AB // CD (cmt)

⇒ AE // DF

Tứ giác AEFD có:

AE // DF (cmt)

AE = DF (cmt)

⇒ AEFD là hình bình hành

Mà ∠DAE = 90⁰ (gt)

⇒ AEFD là hình chữ nhật

c) Do ABCD là hình chữ nhật (gt)

⇒ AB ⊥ CD

⇒ AN ⊥ MF

Tứ giác AMNF có:

D là trung điểm của AN (gt)

D là trung điểm của MF (gt)

⇒ AMNF là hình bình hành

Mà AN ⊥ MF (cmt)

⇒ AMNF là hình thoi

a) \(A=x^2-25\)

\(A=x^2-5^2\)

\(A=\left(x+5\right)\left(x-5\right)\)

Thay x = 105 vào ta có:

\(A=\left(105+5\right)\left(105-5\right)=110\cdot100=11000\)

b) \(B=x^2-4y^2+x-2y\)

\(B=\left(x-2y\right)\left(x+2y\right)+\left(x-2y\right)\)

\(B=\left(x-2y\right)\left(x+2y+1\right)\)

Thay \(x+2y=-1\) vào ta có:

\(B=\left(x-2y\right)\left(-1+1\right)=\left(x-2y\right)\cdot0=0\)

a) \(3\left(x+1\right)+5x=0\)

\(\Leftrightarrow3x+3+5x=0\)

\(\Leftrightarrow8x=-3\)

\(\Leftrightarrow x=-\dfrac{3}{8}\)

b) \(4x^2-1-\left(2x+1\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1-1\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\2x=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\) 

c) \(\left(x+1\right)^2+x^2-1=0\)

\(\Leftrightarrow\left(x+1\right)^2+\left(x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x+1+x-1\right)=0\)

\(\Leftrightarrow\left(x+1\right)2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

d) \(\left(x+2\right)\left(x-2\right)+x\left(x-3\right)-2x^2=8\)

\(\Leftrightarrow x^2-4+x^2-3x-2x^2=8\)

\(\Leftrightarrow-3x-4=8\)

\(\Leftrightarrow-3x=8+4\)

\(\Leftrightarrow-3x=12\)

\(\Leftrightarrow x=-4\)

a) \(x^2-4x^2y^2+y^2+2xy\)

\(=\left(x^2+2xy+y^2\right)-\left(2xy\right)^2\)

\(=\left(x+y\right)^2-\left(2xy\right)^2\)

\(=\left(x-2xy+y\right)\left(x+2xy+y\right)\)

b) \(x^3-x^2y+4x-4y\)

\(=x^2\left(x-y\right)+4\left(x-y\right)\)

\(=\left(x^2+4\right)\left(x-y\right)\)

c) \(x^2+12y-36-y^2\)

\(=x^2-\left(y^2-12y+36\right)\)

\(=x^2-\left(y-6\right)^2\)

\(=\left(x+y-6\right)\left(x-y+6\right)\)

d) \(4x\left(x+y\right)\left(x+y+z\right)\left(x+z\right)+y^2z^2\)

\(=4\left(x^2+xy+xz\right)\left(x^2+xy+xz+yz\right)+y^2z^2\)

\(=4\left(x^2+xy+xz\right)^2+4yz\left(x^2+xy+xz\right)+\left(yz\right)^2\)

\(=\left(2x^2+2xy+2xz+yz\right)^2\)

a, \(x^2\) - 4\(x^2\).y² + y² + 2\(xy\)

 = (\(x^2\) + 2\(xy\) + y²) - (2\(xy\))²

= (\(x\) + y)² - (2\(xy\))²

= (\(x\) + y  - 2\(xy\)).(\(x\) + y + 2\(xy\))

a) \(x\left(x+2\right)-2x\)

\(=x^2+2x-2x\)

\(=x^2\)

b) \(\left(2+x\right)\left(2-x\right)+x^2\)

\(=\left(4-x^2\right)+x^2\)

\(=4-x^2+x^2\)

\(=4\)

c) \(x^2\left(1-x\right)+\left(x+3\right)\left(x^2-3x+9\right)\)

\(=x^2-x^3+x^3+27\)

\(=x^2+27\)

d) \(\left(2x+y\right)^2+4x^2-4x\left(2x+y\right)\)

\(=4x^2+4xy+y^2+4x^2-8x^2-4xy\)

\(=8x^2-8x^2+4xy-4xy+y^2\)

\(=y^2\)

\(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\\ BaCO_3+2HCl\rightarrow BaCl_2+CO_2+H_2O\\ Mg+2HCl\rightarrow MgCl_2+H_2\\ K_2CO_3+H_2SO_4\rightarrow K_2CO_3+CO_2+H_2O\\ Fe_2O_3+6HCl\rightarrow2FeCl_3+3H_2O\\ Cu\left(OH\right)_2+2HNO_3\rightarrow Cu\left(NO_3\right)_2+2H_2O\\ CuO+H_2SO_4\rightarrow CuSO_4+H_2O\\ Ca\left(OH\right)_2+2HCl\rightarrow CaCl_2+2H_2O\)