x2-5x+4=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8)
a) Tam giác ABI và ACK có:
\(\widehat{AIB}=\widehat{AKC}=90^o;\widehat{BAC}\) chung
\(\Rightarrow\Delta ABI\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AI}{AK}\)
\(\Rightarrow\dfrac{AK}{AC}=\dfrac{AI}{AB}\)
Tam giác AIK và ABC có:
\(\dfrac{AK}{AC}=\dfrac{AI}{AB};\widehat{BAC}\) chung
\(\Rightarrow\Delta AIK\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{S_{AIK}}{S_{ABC}}=\left(\dfrac{AI}{AB}\right)^2=cos^2A\)
\(\Rightarrow S_{AIK}=S_{ABC}.cos^2A\)
b) Có \(S_{BCIK}=S_{ABC}-S_{AIK}\)
\(=S_{ABC}-S_{ABC}.cos^2A\)
\(=S_{ABC}\left(1-cos^2A\right)\)
\(=S_{ABC}.sin^2A\)
c) \(S_{HIK}=S_{ABC}-S_{AKI}-S_{BHK}-S_{CHI}\)
\(=S_{ABC}-S_{ABC}.cos^2A-S_{ABC}.cos^2B-S_{ABC}.cos^2C\)
\(=S_{ABC}\left(1-cos^2A-cos^2B-cos^2C\right)\)
d) Có \(cotB=\dfrac{BH}{AH};cotC=\dfrac{CH}{AH}\)
\(\Rightarrow cotB+cotC=\dfrac{BH}{AH}+\dfrac{CH}{AH}=\dfrac{BC}{AH}\)
Nếu \(cotB+cotC\ge\dfrac{2}{3}\) thì \(\dfrac{BC}{AH}\ge\dfrac{2}{3}\Leftrightarrow BC\ge\dfrac{2}{3}AH\)
Nhưng điều này chưa chắc đã đúng tùy vào cách vẽ hình nên bạn cần bổ sung thêm điều kiện gì đó vào câu này nhé.

Gọi thời gian làm riêng để hoàn thành công việc của đội 1 và 2 lần lượt là a, b (ngày)
Điều kiện : a; b > 0
Theo đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{18}\\\dfrac{6}{a}+\dfrac{8}{b}=40\%=\dfrac{2}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{a}=\dfrac{1}{45}\\\dfrac{1}{b}=\dfrac{1}{30}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=45\\b=30\end{matrix}\right.\) (thỏa mãn điều kiện)
Vậy...

Kẻ đường cao BD của tam giác ABC \(\left(D\in AC\right)\)
Khi đó \(AD=AB.cosA=c.cosA\)
\(\Rightarrow CD=AC-AD=b-c.cosA\)
Mặt khác, \(BD=BA.sinA=c\sqrt{1-cos^2A}\)
Tam giác BCD vuông tại D nên:
\(a^2=BC^2=DB^2+DC^2\)
\(=\left(b-c.cosA\right)^2+\left(c\sqrt{1-cos^2A}\right)^2\)
\(=b^2-2bc.cosA+c^2.cos^2A+c^2\left(1-cos^2A\right)\)
\(=b^2+c^2-2bc.cosA\)
Vậy đẳng thức được chứng minh.

Kẻ đường cao AH của tam giác ABC \(\left(H\in BC\right)\). Gọi F là trung điểm của BC.
Khi đó tam giác GBC vuông tại G có trung tuyến GF nên \(GF=\dfrac{1}{2}BC\)
Lại có G là trọng tâm tam giác ABC \(\Rightarrow GF=\dfrac{1}{3}AF\)
\(\Rightarrow\dfrac{1}{2}BC=\dfrac{1}{3}AF\)
\(\Rightarrow\dfrac{AF}{BC}=\dfrac{3}{2}\)
\(\Rightarrow BC=\dfrac{2}{3}AF\) (1)
Mặt khác, tam giác ABH vuông tại H \(\Rightarrow cotB=\dfrac{BH}{AH}\)
Tương tự, \(cotC=\dfrac{CH}{AH}\)
\(\Rightarrow cotB+cotC=\dfrac{BH}{AH}+\dfrac{CH}{AH}=\dfrac{BC}{AH}=\dfrac{\dfrac{2}{3}AF}{AH}\) \(\ge\dfrac{\dfrac{2}{3}AH}{AH}=\dfrac{2}{3}\)
(vì AH, AF là đường vuông góc và đường xiên kẻ từ A đến BC)
Dấu "=" xảy ra \(\Leftrightarrow AH=AF\), nghĩa là đường cao bằng đường trung tuyến ứng với đỉnh A \(\Leftrightarrow\Delta ABC\) cân tại A.
Ta có đpcm.

ĐK: \(a\ne-2\); \(a\in\mathbb{Z}\)
\(P=\dfrac{a-1}{a+2}=\dfrac{a+2-3}{a+2}=1-\dfrac{3}{a+2}\)
Để \(P\in\mathbb{Z}\) thì \(\dfrac{3}{a+2}\in\mathbb{Z}\)
\(\Rightarrow3⋮a+2\)
\(\Rightarrow a+2\inƯ\left(3\right)\)
\(\Rightarrow a+2\in\left\{1;3;-1;-3\right\}\)
\(\Rightarrow a\in\left\{-1;1;-3;-5\right\}\) (tmđk)


Olm chào em, em nên viết bằng công thức toán học nơi có biểu tượng \(\Sigma\) góc trái màn hình em nhé.

Bài 7:
a: ĐKXĐ: \(x\notin\left\{0;1;-1\right\}\)
\(A=\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right):\dfrac{2x}{5x-5}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{5x-5}{2x}\)
\(=\dfrac{x^2+2x+1-x^2+2x-1}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{5\left(x-1\right)}{2x}\)
\(=\dfrac{4x}{\left(x+1\right)}\cdot\dfrac{5}{2x}=\dfrac{10}{x+1}\)
b: Thay x=3 vào A, ta được:
\(A=\dfrac{10}{3+1}=\dfrac{10}{4}=\dfrac{5}{2}\)
Vì x=-1 không thỏa mãn ĐKXĐ
nên Khi x=-1 thì A không có giá trị
c: Đặt A=2
=>\(\dfrac{10}{x+1}=2\)
=>x+1=5
=>x=4(nhận)
Bài 6:
a: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b: \(A=\dfrac{x}{2x-2}+\dfrac{x^2+1}{2-2x^2}\)
\(=\dfrac{x}{2\left(x-1\right)}-\dfrac{x^2+1}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x\left(x+1\right)-x^2-1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{2\left(x+1\right)}\)
c: Đặt A=-1/2
=>\(\dfrac{1}{2\left(x+1\right)}=\dfrac{-1}{2}\)
=>x+1=-1
=>x=-2(nhận)

\(\dfrac{3}{7}x-1=\dfrac{1}{7}x\left(3x-7\right)\)
⇔ \(\dfrac{3}{7}x-\dfrac{7}{7}=\dfrac{3}{7}x^2-\dfrac{7}{7}x\)
⇔ \(\dfrac{3}{7}x-\dfrac{7}{7}-\dfrac{3}{7}x^2+\dfrac{7}{7}x=0\)
⇔ \(\dfrac{3}{7}x\left(1-x\right)-\dfrac{7}{7}\left(1-x\right)=0\)
⇔ \(\left(1-x\right)\left(\dfrac{3}{7}x-\dfrac{7}{7}\right)=0\)
⇔ \(\left[{}\begin{matrix}1-x=0\\\dfrac{3}{7}x-\dfrac{7}{7}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{3}\end{matrix}\right.\)
Vậy pt có 2 nghiệm pt : \(x=1;x=\dfrac{7}{3}\)

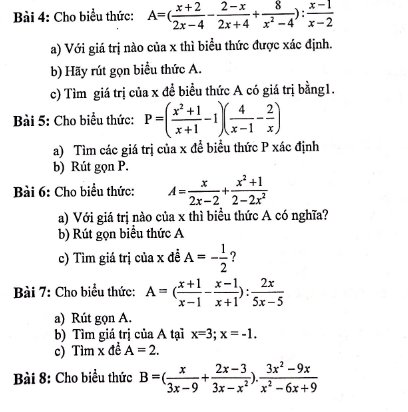
Ta có a + b + c = 1 - 5 + 4 = 0
=> \(x_1=1;x_2=\dfrac{c}{a}=4\)