Đặt \(ƯCLN\left(5m+1,4m+1\right)=d\) (với \(d\inℕ^∗\))

\(\Rightarrow\left\{{}\begin{matrix}5m+1⋮d\\4m+1⋮d\end{matrix}\right.\) 

\(\Rightarrow\left\{{}\begin{matrix}4\left(5m+1\right)⋮d\\5\left(4m+1\right)⋮d\end{matrix}\right.\) 

\(\Rightarrow\left\{{}\begin{matrix}20m+4⋮d\\20m+5⋮d\end{matrix}\right.\) 

\(\Rightarrow\left(20m+5\right)-\left(20m+4\right)⋮d\) 

\(\Rightarrow1⋮d\)

\(\Rightarrow d=1\)

 Vậy \(ƯCLN\left(5m+1,4m+1\right)=1\), suy ra \(5m+1\) và \(4m+1\) là 2 số nguyên tố cùng nhau.

   Gọi ƯCLN(5m+1,4m+1) là d \(\left(d\ne0\right)\) 

=> \(5m+1⋮d;4m+1⋮d\) 

=> \(4\left(5m+1\right)⋮d;5\left(4m+1\right)⋮d\) 

=> \(20m+4⋮d;20m+5⋮d\) 

=> \(\left(20m+5\right)-\left(20m+4\right)⋮d\) 

=> \(1⋮d\) 

=> \(d=1\) 

Vậy 5m +1 và 4m +1 là hai số nguyên tố cùng nhau

\(\text{Miền Trung}\)

miền trung

help 

\(25,4:0,5=50,8\)

\(A=5+5^2+...+5^{30}\)

\(A=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{29}+5^{30}\right)\)

\(A=\left(5+25\right)+5\cdot\left(5+25\right)+...+5^{28}\cdot\left(5+25\right)\)

\(A=30+5\cdot30+...+5^{28}\cdot30\)

\(A=30\cdot\left(1+5+...+5^{28}\right)\)

Vậy A chia hết cho 30

\(A=5+5^2+....+5^{30}\)

\(A=\left(5+5^2+5^3\right)+\left(5^4+5^5+5^6\right)+...+\left(5^{28}+5^{29}+5^{30}\right)\)

\(A=5\cdot\left(1+5+25\right)+5^4\cdot\left(1+5+25\right)+...+5^{28}\cdot\left(1+5+25\right)\)

\(A=5\cdot31+5^4\cdot31+...+5^{28}\cdot31\)

\(A=31\cdot\left(5+5^4+...+5^{28}\right)\)

Vậy A chia hết cho 31

`a,` Ta có `ΔABC` vuông tại `A,`

`=>` `HBA` là góc vuông, có số đo là `90^o`

`b,` Ta có `ΔABC` vuông tại `A`

 `=>` `AH` là đường cao của `ΔABC`

Theo định lý Euclid, trong một tam giác vuông, đường cao chia tam giác thành hai tam giác nhỏ có tỉ lệ bằng độ dài các cạnh gần góc vuông.

Vậy ta có: `(AD)/(AB)` `=` `(HD)/(HC)`

Vì `ΔABC` vuông tại `A`

`=> AB` `= AC`

`=>` `(AD)/(AC)` `=` `(HD)/(HC)`

Nhân cả hai vế của phương trình trên với `AC,` ta có:

`AD .` `(AC)/(AC)` `= HD .` `(HC)/(HC)`

`AD =` `HD.``HC`

`=>`  `AD.AC` `=` `HB.HC.`

a) 90^o,

b).............................. =)  AD.AC = HB.HC

X là ước của 32

 \(Ư\left(32\right)=\left\{1;2;4;8;16;32\right\}\)

Mà: \(10\le X\le25\)

\(\Rightarrow X\in\left\{16\right\}\)

Ước của 32 = {1;2;4;8;16;32}

\(\Rightarrow x=16\)

X chia hết cho 25 vậy X là \(B\left(25\right)\)

\(\Rightarrow X\in B\left(25\right)=\left\{0;25;50;75;100;125;150;...\right\}\)

Mà: X < 100 

Nên:

\(\Rightarrow X\in\left\{0;25;50;75\right\}\)

X chia hết cho 25 vậy X là $B\left(25\right)$

$\Rightarrow X\in B\left(25\right)=\left\{0;25;50;75;100;125;150;...\right\}$

Mà: X < 100  Nên:⇒X∈{0;25;50;75}

Vậy X ∈ {0;25;50;75}

⇒�∈{0;25;50;75}⇒X∈{0;25;50;75}

Ta có 38 chia hết cho X nên X là \(Ư\left(38\right)\)

\(X\inƯ\left(38\right)=\left\{1;2;19;38\right\}\) 

Mà: X > 20

Nên:

\(X\in\left\{38\right\}\)

=>x=38.

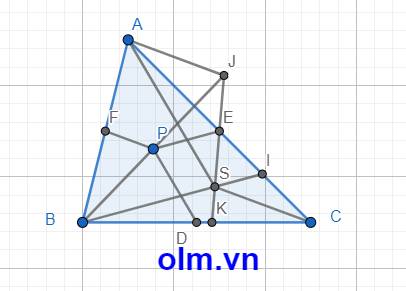
Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:

PE // BS; PE = \(\dfrac{1}{2}\) BS 

⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)

⇒ PJ = PB;  EJ = ES (1)

Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB  theo (1)

⇒  PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)

 ⇒ PF// AJ  (2) 

Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo

     AE = EC (gt)

    EJ = ES ( theo (1)

⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.

⇒ CS // CJ (3)

Kết hợp (2) và(3) ta có:

     CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)

  Kết luận: nếu BS = 2EP thì  CS // PF điều phải chứng minh

3 = 3

4 = 2²

10 = 2.5

BCNN(3; 4; 10) = 2².3.5 = 60

Các bội nhỏ hơn 200 của 3; 4; 10 là:

BC(3; 4; 10) = {0; 60; 120; 180}

\(BCNN\left(3;4;10\right)=30\)

Mà Bội số của 3;4;10 nhỏ hơn 200

\(\Rightarrow BC\left(3;4;10\right)=\left\{0;30;60;90;120;150;180\right\}\)