
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b; 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + ... + \(\dfrac{2}{x\left(x+1\right)}\) = 1\(\dfrac{2023}{2025}\)
\(\dfrac{1}{2}\).(1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + ... + \(\dfrac{2}{x\left(x+1\right)}\)) = \(\dfrac{4048}{2025}\).\(\dfrac{1}{2}\)
\(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.3}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + ... + \(\dfrac{1}{x\left(x+1\right)}\) = \(\dfrac{2024}{2025}\)
\(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + ... + \(\dfrac{1}{x.\left(x+1\right)}\) = \(\dfrac{2024}{2025}\)
\(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + ... + \(\dfrac{1}{x}\) - \(\dfrac{1}{x+1}\) = \(\dfrac{2024}{2025}\)
\(\dfrac{1}{1}\) - \(\dfrac{1}{x+1}\) = \(\dfrac{2024}{2025}\)
\(\dfrac{1}{x+1}\) = 1 - \(\dfrac{2024}{2025}\)
\(\dfrac{1}{x+1}\) = \(\dfrac{1}{2025}\)
\(x+1\) = 2025
\(x\) = 2025 - 1
\(x=2024\)
Vậy \(x=2024\)

\(S=\dfrac{2}{3}\times\dfrac{4}{5}\times...\times\dfrac{4046}{4047}\)
\(S< \dfrac{3}{4}\times\dfrac{5}{6}\times...\times\dfrac{4047}{4048}\)
\(S^2< \dfrac{2}{3}\times\dfrac{4}{5}\times...\times\dfrac{4046}{4047}\times\left(\dfrac{3}{4}\times\dfrac{5}{6}\times...\times\dfrac{4047}{4048}\right)\)
\(S^2< \dfrac{2\times3\times4\times5\times...\times4046\times4047}{3\times4\times5\times6\times...\times4047\times4048}\)
\(S^2< \dfrac{2}{4048}\)
⇒ \(S^2< \dfrac{1}{2024}\)

Chương trình là gì tập hợp các lệnh viết bằng ngôn ngữ lập trình nào đó, chỉ dẫn theo từng bước của thuật toán để máy tính thức hiện được.

\(C=\dfrac{4}{3\cdot5}+\dfrac{4}{5\cdot7}+\dots+\dfrac{4}{97\cdot99}\)
\(=2\cdot\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dots+\dfrac{2}{97\cdot99}\right)\)
\(=2\cdot\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dots+\dfrac{1}{97}-\dfrac{1}{99}\right)\)
\(=2\cdot\left(\dfrac{1}{3}-\dfrac{1}{99}\right)\)
\(=2\cdot\dfrac{32}{99}=\dfrac{64}{99}\)
\(D=\dfrac{18}{2\cdot5}+\dfrac{18}{5\cdot8}+\dots+\dfrac{18}{203\cdot206}\)
\(=6\cdot\left(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+\dots+\dfrac{3}{203\cdot206}\right)\)
\(=6\cdot\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dots+\dfrac{1}{203}-\dfrac{1}{206}\right)\)
\(=6\cdot\left(\dfrac{1}{2}-\dfrac{1}{206}\right)\)
\(=6\cdot\dfrac{51}{103}=\dfrac{306}{103}\)
Khi đó: \(\dfrac{C}{D}=\dfrac{\dfrac{64}{99}}{\dfrac{306}{103}}=\dfrac{3296}{15147}\)

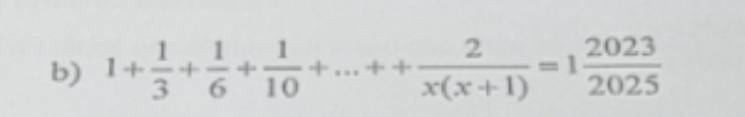
Câu 4:
a: O nằm trên tia đối của tia AB
=>A nằm giữa O và B
=>OB=OA+AB
=>OB=4+6=10(cm)
M là trung điểm của OA
=>\(OM=MA=\dfrac{OA}{2}\)
N là trung điểm của OB
=>\(ON=NB=\dfrac{OB}{2}\)
Vì OA<OB
nên OM<ON
=>M nằm giữa O và N
=>OM+MN=ON
=>\(MN=ON-OM=\dfrac{OB}{2}-\dfrac{OA}{2}=\dfrac{10}{2}-\dfrac{4}{2}=5-2=3\left(cm\right)\)
b: \(MN=ON-OM=\dfrac{OB}{2}-\dfrac{OA}{2}=\dfrac{1}{2}\left(OB-OA\right)\)
\(=\dfrac{1}{2}\cdot AB\) không đổi khi O di chuyển trên tia đối của tia AB