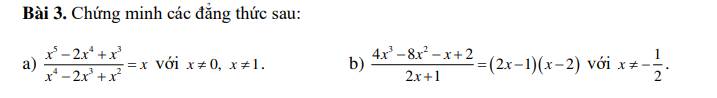
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{3}{4ab^2}=\dfrac{3\cdot5a}{4ab^2\cdot5a}=\dfrac{15a}{20a^2b^2}\)
\(\dfrac{4}{5a^2b}=\dfrac{4\cdot4b}{5a^2b\cdot4b}=\dfrac{16b}{20a^2b^2}\)
b) \(\dfrac{x}{2x+6}=\dfrac{x}{2\left(x+3\right)}=\dfrac{x\left(x-3\right)}{2\left(x+3\right)\left(x-3\right)}\)
\(\dfrac{4}{x^2-9}=\dfrac{4}{\left(x+3\right)\left(x-3\right)}=\dfrac{8}{2\left(x+3\right)\left(x-3\right)}\)
c) \(\dfrac{2x}{x^3-1}=\dfrac{2x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\dfrac{x+1}{x^2+x+1}=\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
d) \(\dfrac{x}{x^2+2x-3}=\dfrac{x}{\left(x-1\right)\left(x+3\right)}=\dfrac{x\left(x-1\right)}{\left(x-1\right)^2\left(x+3\right)}\)
\(\dfrac{3x}{x^2-2x+1}=\dfrac{3x}{\left(x-1\right)^2}=\dfrac{3x\left(x+3\right)}{\left(x-1\right)^2\left(x+3\right)}\)
\(\dfrac{-4}{x+3}=\dfrac{-4\left(x-1\right)^2}{\left(x-1\right)^2\left(x+3\right)}\)

a) \(M=\dfrac{15x^2y^3}{30xy^3z^2}=\dfrac{15xy^3\cdot x}{15xy^3\cdot2z^2}=\dfrac{x}{2z^2}\left(x;y;z\ne0\right)\)
b) \(N=\dfrac{x^4-4x^2}{x^2-4}=\dfrac{x^2\left(x^2-4\right)}{x^2-4}=x^2\left(x\ne\pm2\right)\)
c) \(P=\dfrac{x^3-3x^2+3x-1}{x^2-2x+1}=\dfrac{x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3}{x^2-2\cdot x\cdot1+1^2}=\dfrac{\left(x-1\right)^3}{\left(x-1\right)^2}=x-1\left(x\ne1\right)\)
d) \(A=\dfrac{\left(2x^2+2x\right)\left(x-2\right)^2}{\left(x^3-4x\right)\left(x+1\right)}=\dfrac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x^2-4\right)\left(x+1\right)}=\dfrac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x+2\right)\left(x-2\right)\left(x+1\right)}=\dfrac{2\left(x-2\right)}{x+2}\left(x\ne0;x\ne\pm2;x\ne-1\right)\)e) \(B=\dfrac{x^3-x^2y+xy^2}{x^3+y^3}=\dfrac{x\left(x^2-xy+y^2\right)}{\left(x+y\right)\left(x^2-xy+y^2\right)}=\dfrac{x}{x+y}\left(x\ne-y\right)\)

Cần lưu ý nhé: HCl, HNO3 và H2SO4 là axit chứ không phải là bazơ, KCl mang tính trung tính vì là chất này được tạo từ cả bazơ mạnh lẫn axit mạnh. C2H5OH là chất điện li nên cũng không phải là bazơ
a)
- Những chất là bazơ tan:
+ NaOH
+ KOH
+ Ba (OH)2
- Những chất là bazơ không tan:
+ Cu(OH)2
+ Fe(OH)3
+ Mg(OH)2
b)
NaOH: Natri Hidroxide
KCl: Kali Clohidric
HCl: Axit Clohidric
HNO3: Axit Nitric
Cu (OH)2: Đồng (II) Hidroxide
Fe(OH)3: Sắt (III) Hidroxide
MgSO4: Magiê Surfuric
H2SO4: Axit Surfuric
KOH: Kali Hidroxide
Ba(OH)2: Bari Hidroxide
C2H5OH: Ancol Etylic
Mg(OH)2: Magiê Hidroxide
#HT


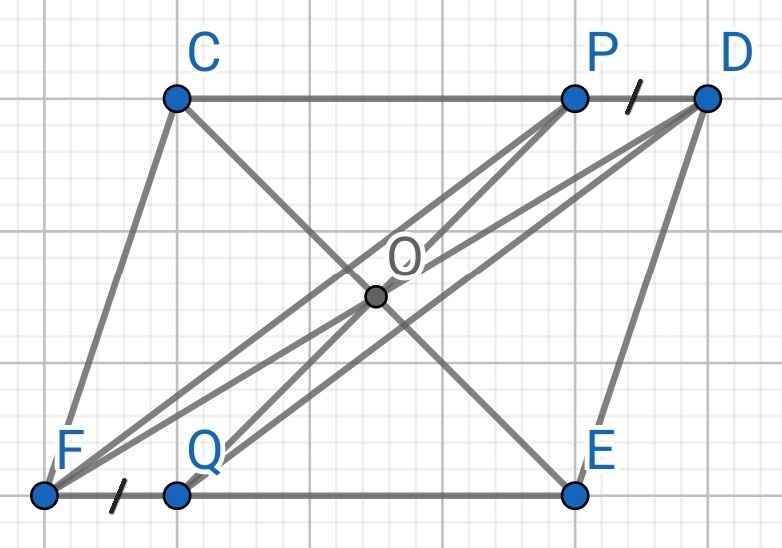 a) Sửa đề: Chứng minh PF // DQ
a) Sửa đề: Chứng minh PF // DQ
Do CDEF là hình bình hành (gt)
⇒ CD // EF
⇒ DP // FQ
Tứ giác DPFQ có:
DP // FQ (cmt)
DP = FQ (gt)
⇒ DPFQ là hình bình hành
⇒ PF // DQ
b) Do CDEF là hình bình hành (gt)
O là trung điểm của CE (gt)
⇒ O là trung điểm của DF
Mà DPFQ là hình bình hành
⇒ O là trung điểm của PQ

Vườn ông minh là hình vuông
Cạnh hình vuông là: 20 : 4 = 5 (m)
Chiều rộng hình chữ nhật sau khi tăng là: 5 + y (m)
Chiều dài hình chữ nhật sau khi tăng là: 8\(x\) (m)
Diện tích hình chữ nhật sau khi tăng là: 8\(x\).(5 + y) (m2)

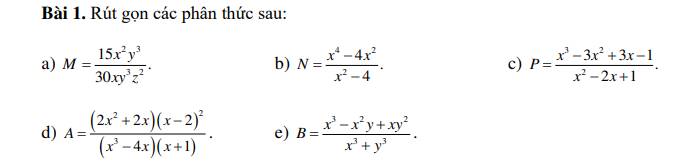
\(a,\dfrac{x^5-2x^4+x^3}{x^4-2x^3+x^2}=\dfrac{x^3\left(x^2-2x+1\right)}{x^2\left(x^2-2x+1\right)}=\dfrac{x.x^2\left(x-1\right)^2}{x^2\left(x-1\right)^2}=x\left(đpcm\right)\\ b,\dfrac{4x^3-8x^2-x+2}{2x+1}=\dfrac{4x^2\left(x-2\right)-\left(x-2\right)}{2x+1}\\ =\dfrac{\left(4x^2-1\right)\left(x-2\right)}{2x+1}=\dfrac{\left(2x+1\right)\left(2x-1\right)\left(x-2\right)}{2x+1}=\left(2x-1\right)\left(x-2\right)\left(đpcm\right)\)
\(a,VT=\dfrac{x^5-2x^4+x^3}{x^4-2x^3+x^2}=\dfrac{x\left(x^4-2x^3+x^2\right)}{x^4-2x^3+x^2}=x=VP\left(x\ne0;x\ne1\right)\)
\(b,VT=\dfrac{4x^3-8x^2-x+2}{2x+1}\left(x\ne-\dfrac{1}{2}\right)\)
\(=\dfrac{4x^2\left(x-2\right)-\left(x-2\right)}{2x+1}\)
\(=\dfrac{\left(4x^2-1\right)\left(x-2\right)}{2x+1}\)
\(=\dfrac{\left(2x-1\right)\left(2x+1\right)\left(x-2\right)}{2x+1}\)
\(=\left(2x-1\right)\left(x-2\right)=VP\)
\(\text{#}Toru\)