Ta có: \(\dfrac{a}{1+9b^2}=a-\dfrac{9ab^2}{1+9b^2}\ge a-\dfrac{3ab}{2}\)

\(\Rightarrow\)\(\text{Σ}\dfrac{a}{1+9b^2}\ge a+b+c-\dfrac{3\left(ab+bc+ca\right)}{2}\ge a+b+c-\dfrac{\left(a+b+c\right)^2}{2}=\dfrac{1}{2}\)

(Áp dụng BĐT Cô Si cho 2 số dương, ta có:

\(\text{ }ab+bc+ca\le a^2+b^2+c^2\Rightarrow3\left(\text{ }ab+bc+ca\right)\le\left(a+b+c\right)^2\))

Dấu "=" xảy ra \(\Leftrightarrow a=b=c=\dfrac{1}{3}\)

Gọi số máy tổ I và tổ II sản xuất được lần lượt là \(a,b\left(a,b\inℕ^∗;a,b< 860\right)\)ta có:

\(\left\{{}\begin{matrix}a+b=860\\\left(a+15\%a\right)+\left(b+10\%b\right)=964\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\\left(a+b\right)+\left(15\%a+10\%b\right)=964\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\860+\left(15\%a+10\%b\right)=964\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\15\%a+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%a+5\%a+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%\left(a+b\right)+5\%a=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%\cdot860+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\86+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%b=18\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\b=180\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}b=180\\a=a+b-b=860-180\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}b=180\\a=680\end{matrix}\right.\)

Vậy tổ 1 sản xuất được 680 máy trong tháng đầu, tổ 2 sản xuất được 180 máy trong tháng đầu.

Phương trình hoành độ giao điểm

x² = -x + 2

<=> x² + x - 2 = 0

Nhận thấy phương trình có a + b + c = 0 nên phương trình có 2 nghiệm \(x_1=1;x_2=-2\)

Với x₁ = 1 => y₁ = 1 => A(1,1) 

Với x₂ = -2 => y₂ = 4 => B(-2 , 4) 

Ta có BO = \(\sqrt{\left(-2\right)^2+4^2}=\sqrt{20}\);

\(OA=\sqrt{1^2+1^2}=\sqrt{2}\)

AB = \(\sqrt{3^2+3^2}=\sqrt{18}\)

Từ đó dễ thấy OA² + AB² = BO² 

=> Tam giác AOB vuông tại A

nên S_AOB = \(\dfrac{\sqrt{18}.\sqrt{2}}{2}=3\)

x² = -x + 2

<=> x² + x - 2 = 0

Nhận thấy phương trình có a + b + c = 0 nên phương trình có 2 nghiệm 

Với x₁ = 1 => y₁ = 1 => A(1,1) 

Với x₂ = -2 => y₂ = 4 => B(-2 , 4) 

Ta có BO = ;

AB = 

Từ đó dễ thấy OA² + AB² = BO² 

=> Tam giác AOB vuông tại A

nên S_AOB = 

Kết quả đây em nhé @Nguyên●   Trong "Làng", chi tiết kể về ông Hai cứ múa tay lên mà khoe nhà ông bị đốt nhẵn… Mới đọc chi tiết này, ta thấy dường như vô lý bởi ngôi nhà là cả một tài sản quá lớn. Hơn thế nó còn gắn với bao kỷ niệm vui buồn rất thiêng liêng của mỗi con người. Mất nó ai mà không xót xa đau đớn?

●   Nhưng ông Hai lại có cử chỉ “Múa tay lên để khoe" đó là biểu hiện của tâm trạng sung sướng, sung sướng đến tột độ. Tâm trạng này dường như có vẻ không bình thường? Không ! Đặt ông Hai trong hoàn cảnh của "Làng", làng Dầu đang bị tai tiếng việt gian theo tây thì ông Hai vui sướng sao được vì nhà bị tây đốt là bằng chứng hùng hồn rằng làng Dầu của ông vẫn theo kháng chiến, theo cách mạng, đó là một làng quê anh hùng, đứng dậy chống thực dân Pháp.

●   Chắc hẳn mất nhà ông Hai cũng đau lắm chứ, xót xa lắm chứ. Nhưng dù thế nào thì nhà còn có thể xây dựng lại được, song danh dự của làng đâu dễ lấy lại? Ông đã quên sự mất mát riêng để tự hào sung sướng trong vẻ đẹp, sức mạnh chung của làng quê, đất nước. Niềm vui, nỗi buồn của ông Hai luôn gắn liền với vận mệnh của Làng Dầu.

●   Thế mới biết ông Hai yêu làng quê tha thiết đến chừng nào! Tình yêu làng quê được mở rộng, hoà quện trong tình yêu tổ quốc thật sâu nặng và thiêng liêng.

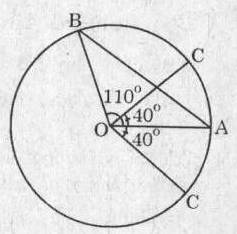
Theo giả thiết: Vì số đo cung \(\stackrel\frown{AC}=40^o\)

\(\Rightarrow\) Góc ở tâm \(\widehat{AOC}=40^o\)

Trường hợp 1: C thuộc cung nhỏ \(\stackrel\frown{AB}\)

- Số đo góc ở tâm \(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}=110^o-40^o=70^o\)

Do vậy:

- Số đo cung nhỏ \(\stackrel\frown{BC}=70^o\)

- Số đo cung lớn \(\stackrel\frown{BC}=360^o-70^o=290^o\)

Trường hợp 2: C thuộc cung lớn \(\stackrel\frown{BC}\)

- Số đo góc ở tâm \(\widehat{BOC}=\widehat{BOA}+\widehat{AOC}=110^o+40^o=150^o\)

Do vậy:

- Số đo cung nhỏ \(\stackrel\frown{BC}=150^o\)

- Số đo cung lớn \(\stackrel\frown{BC}=360^o-150^o=210^o\)