Cho Parabol 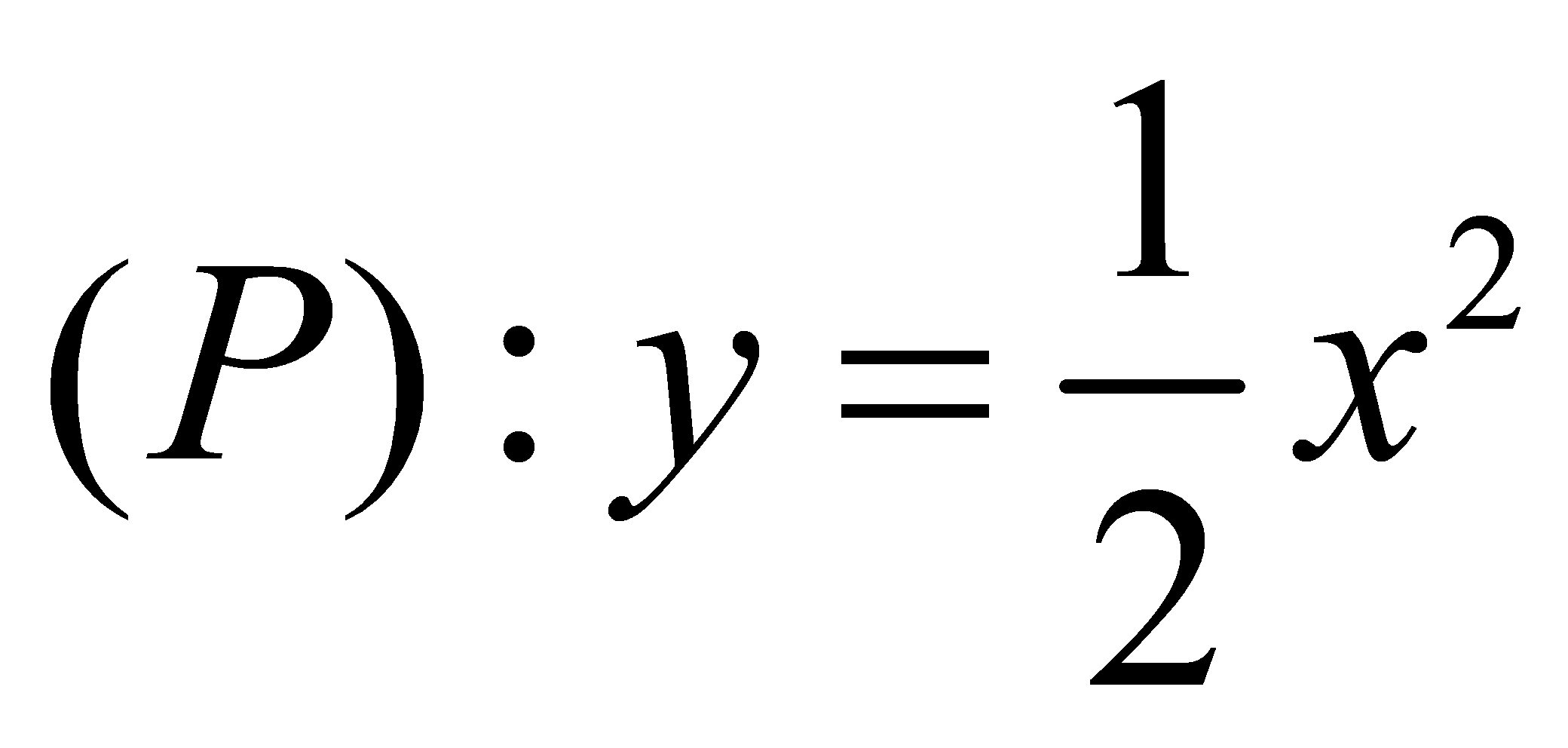 và đường thẳng
và đường thẳng 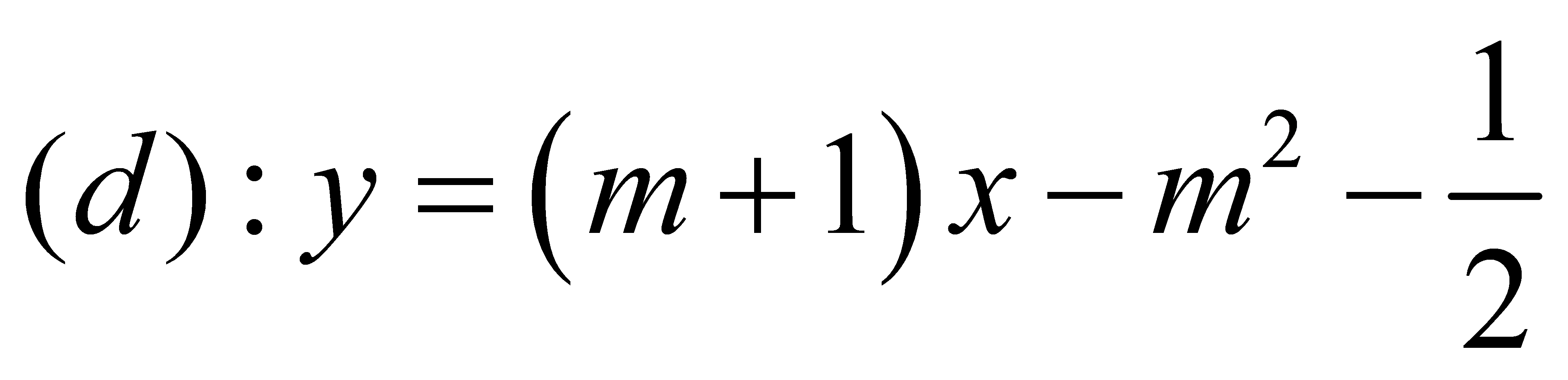 (
(![]() là tham số). Có bao nhiêu giá trị nguyên dương của
là tham số). Có bao nhiêu giá trị nguyên dương của ![]() thì đường thẳng
thì đường thẳng ![]() cắt Parabol
cắt Parabol ![]() tại hai điểm
tại hai điểm ![]() sao cho biểu thức
sao cho biểu thức ![]() đạt giá trị nhỏ nhất?
đạt giá trị nhỏ nhất?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a2 + b2 + c2 = ab + bc + ca
<=> 2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ca
<=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca = 0
<=> (a2 - 2ab + b2) + (a2 - 2ca + c2) + (b2 - 2bc + c2) = 0
<=> (a - b)2 + (a - c)2 + (b - c)2 = 0
<=> \(\hept{\begin{cases}a-b=0\\a-c=0\\b-c=0\end{cases}}\Leftrightarrow a=b=c\)(đpcm)
Nhân vế 2 biểu thức, ta có:
\(2a^2+2b^2+2c^2=2ab+2bc+2ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab+2bc+2ca=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\left(1\right)\)
Vì\(\left(a-b\right)^2\ge0;\left(b-c\right)^2\ge0;\left(c-a\right)^2\ge0\)nên từ (1) \(\Rightarrow a-b=b-c=c-a=0\)hay \(a=b=c\)

Ta có:\(\frac{1}{ab}+\frac{1}{cd}\ge\frac{8}{\left(a+b\right)\left(c+d\right)}\Leftrightarrow\left(\frac{1}{ab}+\frac{1}{cd}\right)\left(a+b\right)\left(c+d\right)\ge8\)
Xét bất đẳng thức Cô si
\(\hept{\begin{cases}\frac{1}{ab}+\frac{1}{cd}\ge2\sqrt{\frac{1}{abcd}}\\a+b\ge2\sqrt{ab}\\c+d\ge2\sqrt{cd}\end{cases}}\)
\(\Rightarrow\left(\frac{1}{ab}+\frac{1}{cd}\right)\left(a+b\right)\left(c+d\right)\ge2\cdot\frac{1}{\sqrt{abcd}}\cdot2\sqrt{ab}\cdot2\sqrt{cd}\)
\(\Rightarrow\left(\frac{1}{ab}+\frac{1}{cd}\right)\left(a+b\right)\left(c+d\right)\ge8\left(đpcm\right)\)
Dấu "=" xảy ra khi\(\hept{\begin{cases}\frac{1}{ab}=\frac{1}{cd}\\a=b\\c=d\end{cases}}\Leftrightarrow a=b=c=d\)

Mình thì dư đoán điểm rơi \(a=b=c=1\) rồi, nhưng nháp mãi vẫn không ra được.
\(\frac{a}{b^3+ab}\)=\(\frac{a^2}{b^3a+a^2b}\)
tương tự thì ta có S= \(\frac{a^2}{b^3a+a^2b}\) + \(\frac{b^2}{c^3b+b^2c}\) + \(\frac{c^2}{a^3c+ac^2}\)
áp dụng bất dẳng thức cô si s goát,ta có
S=\(\frac{a^2}{b^3a+a^2b}\)+ \(\frac{b^2}{c^3b+b^2c}\)+ \(\frac{c^2}{a^3c+ac^2}\)\(\ge\) \(\frac{\left(a+b+c\right)^2}{b^3a+a^2b+c^3b+b^2c+a^3c+c^2a}\)
cái mẫu mk chx nghĩ ra phân tích ra sao nx,tí nghĩ nốt


b) Ta có \(A=\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}\ge\frac{\left(x+y+z\right)^2}{y+z+z+x+x+y}\)(BĐT Schwarz)
\(=\frac{x+y+z}{2}=\frac{2}{2}=1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\frac{x^2}{y+z}=\frac{y^2}{z+x}=\frac{z^2}{x+y}\\x+y+z=2\end{cases}}\Leftrightarrow x=y=z=\frac{2}{3}\)
a) Có \(P=1.\sqrt{2x+yz}+1.\sqrt{2y+xz}+1.\sqrt{2z+xy}\)
\(\le\sqrt{\left(1^2+1^2+1^2\right)\left(2x+yz+2y+xz+2z+xy\right)}\)(BĐT Bunyakovsky)
\(=\sqrt{3.\left[2\left(x+y+z\right)+xy+yz+zx\right]}\)
\(\le\sqrt{3\left[4+\frac{\left(x+y+z\right)^2}{3}\right]}=\sqrt{3\left(4+\frac{4}{3}\right)}=4\)
Dấu "=" xảy ra <=> x = y = z = 2/3

a, Xét tam giác ATB và tam giác ACT ta có :
^A _ chung
^ATB = ^BCT ( cùng chắn cung TB )
Vậy tam giác ATB~ tam giác ACT (g.g )
=> \(\frac{AT}{AC}=\frac{AB}{AT}\Rightarrow AT^2=AB.AC\)(1)
b, Vì AT là tiếp tuyến đường tròn (O)
=> ^ATO = 900
Xét tam giác ATO vuông tại T, đường cao TH ta có :
\(AT^2=AH.AO\)( hệ thức lượng ) (2)
Từ (1) ; (2) ta có đpcm
\(\Rightarrow\frac{AC}{AH}=\frac{AO}{AB}\)
c, Xét tam giác ACO và tam giác AHB ta có :
^A _ chung
\(\frac{AC}{AH}=\frac{AO}{AB}\left(cmt\right)\)
Vậy tam giác ACO ~ tam giác AHB (c.g.c)
=> ^ACO = ^AHB ( 2 góc tương ứng )

a, Thay m = 2 ta được
\(\hept{\begin{cases}x+2y=1\\2x+y=2\end{cases}}\Leftrightarrow\hept{\begin{cases}2x+4y=2\\2x+y=2\end{cases}}\Leftrightarrow\hept{\begin{cases}y=0\\x=1\end{cases}}\)
b, Để hpt có nghiệm duy nhất khi \(\frac{1}{m}\ne\frac{m}{1}\Leftrightarrow m\ne1\)
