Ta có a: 6 dư 5
=> a= 6k+5 với k ϵ N
có: a² = (6k+5)² = 36k²+ 60k+25
vì 36k²⋮6 ; 60k⋮6 ; 25 : 6 dư 1
=> a² chia 6 dư 1 
 

Lời giải:

Vì $a$ chia $6$ dư $5$ nên đặt $a=6k+5$ với $k$ nguyên. 

Khi đó: $a^2=(6k+5)^2=36k^2+25+60k=6(6k^2+10k+4)+1$ chia $6$ dư $1$

\((x-y+2)^2\\=x^2+y^2+2^2-2xy-2\cdot y\cdot2+2\cdot x\cdot2\\=x^2+y^2+4-2xy-4y+4x\)

1 We've them out of run

2 If you across it come tell me

3 you should look up it

4 My friend came up with it

5 so don't throw them away

1 run our of them

2 if you come across it

3 you should look it up

4 my friend came up with it

5 so don't throw them away

1 B

2 D

3 B

4 A

5 B

6 C

7 A

\(\dfrac{4x+2}{4x-2}+\dfrac{3-6x}{6x-6}\left(dkxd:x\ne\dfrac{1}{2};x\ne1\right)\)

\(=\dfrac{2\left(2x+1\right)}{2\left(2x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)

\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2\left(x-1\right)}\)

\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2x-2}\)

\(=\dfrac{\left(2x+1\right)\left(2x-2\right)}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{\left(1-2x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{4x^2-2x-2}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{4x^2-2x-2-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{2x-3}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{2x-3}{4x^2-6x+2}\)

\(x\) + 2y = 8

\(2y\)        = 8 - \(x\)

 y        = \(\dfrac{8-x}{2}\)

  y =  - \(\dfrac{x}{2}\) + 4

Thay y = - \(\dfrac{x}{2}\) + 4 vào biểu thức B = \(xy\) ta có: 

B = \(x\).(-\(\dfrac{x}{2}\) + 4)

B = - \(\dfrac{x^2}{2}\) + 4\(x\)

B = -\(\dfrac{1}{2}\). (\(x^2\)  - 8\(x\)  + 16)  +  8 

B = - \(\dfrac{1}{2}\).(\(x\) - 4)² + 8

Vì  \(\dfrac{1}{2}\).(\(x\) - 4)² ≥ 0 ⇒ - \(\dfrac{1}{2}\).(\(x\) - 4)² ≤ 0 ⇒ - \(\dfrac{1}{2}\).(\(x\)  - 4)² + 8 ≤ 8

Dấu bằng xảy ra khi:  \(x\) - 4 = 0 ⇒ \(x\) = 4; thay \(x\) = 4 vào biểu thức:

y = - \(\dfrac{1}{2}\) \(x\)+ 4 ta có y = - \(\dfrac{4}{2}\) + 4 = 2

Vậy giá trị lớn nhất của B là 8 xảy ra khi \(x\) = 4; y = 2

Chào các bạn ! Cho mình hỏi là nhân vật chính trong câu chuyện cây vú sữa là ai ? Giúp mình với.Mong các bạn phản hồi sớm.Cảm ơn

A.Cậu bé

B.Người mẹ

C.Người mẹ và cậu bé

D.Mọi người

A.Cậu bé

Olm chào em. Cảm ơn em đã đồng hành cùng olm trong thời gian qua.

Hiện nay olm cũng đang bổ sung và cập nhật rất nhiều video mới. Dự định sẽ up load trong thời gian tới.

Chúc em học tập vui vẻ và hiệu quả cùng olm em nhé!

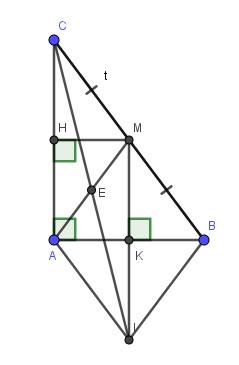
a) Do \(MH\perp AC\left(gt\right)\)

\(\Rightarrow\widehat{MHA}=90^0\)

Do \(MK\perp AB\left(gt\right)\)

\(\Rightarrow\widehat{MKA}=90^0\)

Do \(\Delta ABC\) vuông tại A

\(\Rightarrow\widehat{CAB}=90^0\)

\(\Rightarrow\widehat{HAK}=90^0\)

Tứ giác \(AKMH\) có:

\(\widehat{MHA}=\widehat{HAK}=\widehat{MKA}=90^0\)

\(\Rightarrow AKMH\) là hình chữ nhật

b) Do \(MK\perp AB\left(cmt\right)\)

Mà \(AB\perp AC\) (\(\Delta ABC\) vuông tại A)

\(\Rightarrow MK\) // \(AC\)

Mà \(M\) là trung điểm của BC

\(\Rightarrow K\) là trung điểm của AB

Tứ giác AMBI có:

K là trung điểm của AB (cmt)

K là trung điểm của MI (gt)

\(\Rightarrow AMBI\) là hình bình hành

\(\Rightarrow AI=BM\)

Mà \(BM=CM\) (do M là trung điểm của BC)

\(\Rightarrow AI=CM\)

Do \(AMBI\) là hình bình hành (cmt)

\(\Rightarrow AI\) // \(BM\)

\(\Rightarrow AI\) // \(CM\)

Tứ giác \(ACMI\) có:

\(AI\) // \(CM\left(cmt\right)\)

\(AI=CM\left(cmt\right)\)

\(\Rightarrow ACMI\) là hình bình hành

Mà E là trung điểm của AM

\(\Rightarrow\) E là trung điểm của CI

Hay C, E, I thẳng hàng

c) Để \(AKMH\) là hình vuông thì:

\(MH=MK\) (1)

Do \(MH\perp AC\) (cmt)

\(AC\perp AB\left(cmt\right)\)

\(\Rightarrow MH\) // \(AB\)

Mà M là trung điểm của BC

\(\Rightarrow H\) là trung điểm của AC

\(\Rightarrow MH\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MH=\dfrac{AB}{2}\) (2)

Lại có:

M là trung điểm của BC (cmt)

K là trung điểm của AB (cmt)

\(\Rightarrow MK\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MK=\dfrac{AC}{2}\) (3)

Từ (1), (2), (3) \(\Rightarrow AB=AC\)

\(\Rightarrow\Delta ABC\) cân tại A

Vậy để AKMH là hình vuông thì \(\Delta ABC\) vuông cân tại A

giúp em với ạ em cảm ơn