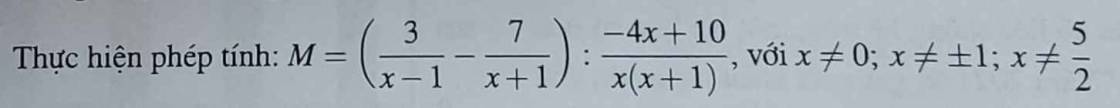 giúp mình câu này vs ạ
giúp mình câu này vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 the
2 0
3 a - the
4 a
5 the
6 a
7 0
8 the - the
9 a
10 0
11 the
12 0
13 the
14 the
15 0 - 0
16 the
17 the - 0
18 0
19 a - an
20 the - the - the - the
21 0 - 0
22 the - the

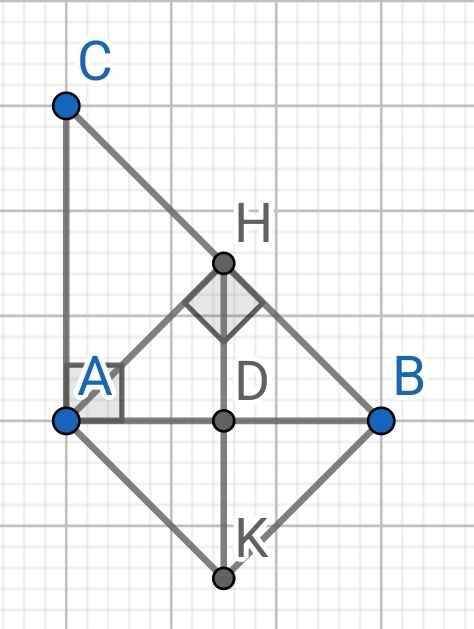
Do AH ⊥ BC (gt)
⇒ AH ⊥ BH
Do ∆ABC vuông cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Gọi D là giao điểm của AB và HK
Do H và K đối xứng nhau qua AB (gt)
⇒ D là trung điểm của HK và AB là đường trung trực của HK
⇒ HK ⊥ AB
Mà AB ⊥ AC
⇒ HK // AC
⇒ HD // AC
Mà H là trung điểm của BC
⇒ D là trung điểm AB
Do ∆ABC vuông cân tại A (gt)
AH là đường trung tuyến của ∆ABC (cmt)
⇒ AH = HB = HC = BC : 2
Tứ giác AHBK có:
D là trung điểm HK (cmt)
D là trung điểm AB (cmt)
⇒ AHBK là hình bình hành
Mà AH ⊥ BH (cmt)
⇒ AHBK là hình chữ nhật
Lại có AH = BH (cmt)
⇒ AHBK là hình vuông

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn.

a) ĐKXĐ: x\(\ne\)0, x\(\ne\)2
Ta có:
A= 2x-4/ x2- 2x = 2(x-2)/ x(x-2) = 2/x
Vậy...
b) Ta thấy x=26 thỏa mãn ĐKXĐ
Thay x=26 vào bt A ta được
A= 2/26 = 1/13
Vậy....
c) Với x\(\ne\)0, x\(\ne\)2 ta có A=12 \(\Leftrightarrow\) 2/x =12 \(\Leftrightarrow\) x=1/6
Vậy....

\(x^2\) - 8\(x\) + 19
= (\(x^2\) -2.\(x\) . 4 + 42) + 3
= (\(x\) - 4)2 + 3
Vì (\(x\) - 4)2 ≥ 0 ∀ \(x\) ⇒ (\(x\) - 4)2 + 3 ≥ 3 dấu bằng xảy ra khi
\(x\) - 4 = 0 ⇒ \(x\) = 4
Vậy giá trị nhỏ nhất của \(x^2\) - 8\(x\) + 19 là 3 xảy ra .khi \(x\) = 4

Q = x^2 + 8x + 20
= (x^2 + 8x + 16) + 4
= (x+4)^2 + 4 ≥ 4 với mọi x
Dấu = xảy ra khi :
x+4=0 hay x = -4
VẬY MIN Q = 4 tại x = -4
Q = x2+ 8x + 20
= x2+ 2.4.x + 16+ 4
= (x+4)2+4
Vì (x+4)2 \(\ge\) 0 với mọi x \(\Rightarrow\) (x+4)2+ 4\(\ge\) 0+4
hay Q\(\ge\) 4
Dấu "=" xảy ra \(\Leftrightarrow\) (x+4)2=0 \(\Leftrightarrow\) x+4=0 \(\Leftrightarrow\) x= -4
Vậy Q đạt giá trị nhỏ nhất khi x= -4

a, Ta có: \(n_{Na}=\dfrac{2,3}{23}=0,1\left(mol\right)\)
\(m_{HCl}=60.7,3\%=4,38\left(g\right)\Rightarrow n_{HCl}=\dfrac{4,38}{36,5}=0,12\left(mol\right)\)
PT: \(2Na+2HCl\rightarrow2NaCl+H_2\)
Xét tỉ lệ: \(\dfrac{0,1}{2}< \dfrac{0,12}{2}\), ta được HCl dư.
Theo PT: \(n_{H_2}=\dfrac{1}{2}n_{Na}=0,05\left(mol\right)\Rightarrow V_{H_2}=0,05.24,79=1,2395\left(l\right)\)
b, \(n_{HCl\left(pư\right)}=n_{NaCl}=n_{Na}=0,1\left(mol\right)\)
\(\Rightarrow n_{HCl\left(dư\right)}=0,12-0,1=0,02\left(mol\right)\)
Ta có: m dd sau pư = 2,3 + 60 - 0,05.2 = 62,2 (g)
\(\Rightarrow\left\{{}\begin{matrix}C\%_{NaCl}=\dfrac{0,1.58,5}{62,2}.100\%\approx9,41\%\\C\%_{HCl}=\dfrac{0,02.36,5}{62,2}.100\%\approx1,17\%\end{matrix}\right.\)
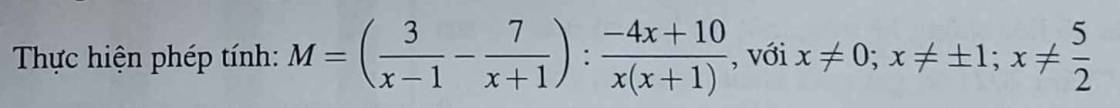
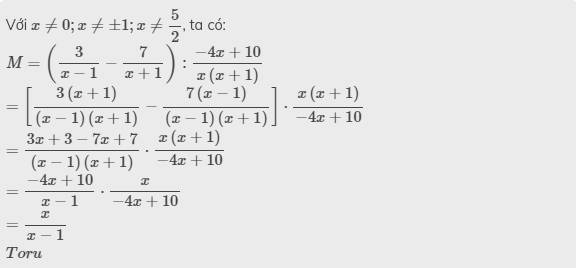
Với \(x\ne0;x\ne\pm1;x\ne\dfrac{5}{2}\), ta có:
\(M=\left(\dfrac{3}{x-1}-\dfrac{7}{x+1}\right):\dfrac{-4x+10}{x\left(x+1\right)}\)
\(=\left[\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}-\dfrac{7\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{3x+3-7x+7}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{-4x+10}{x-1}\cdot\dfrac{x}{-4x+10}\)
\(=\dfrac{x}{x-1}\)
\(Toru\)