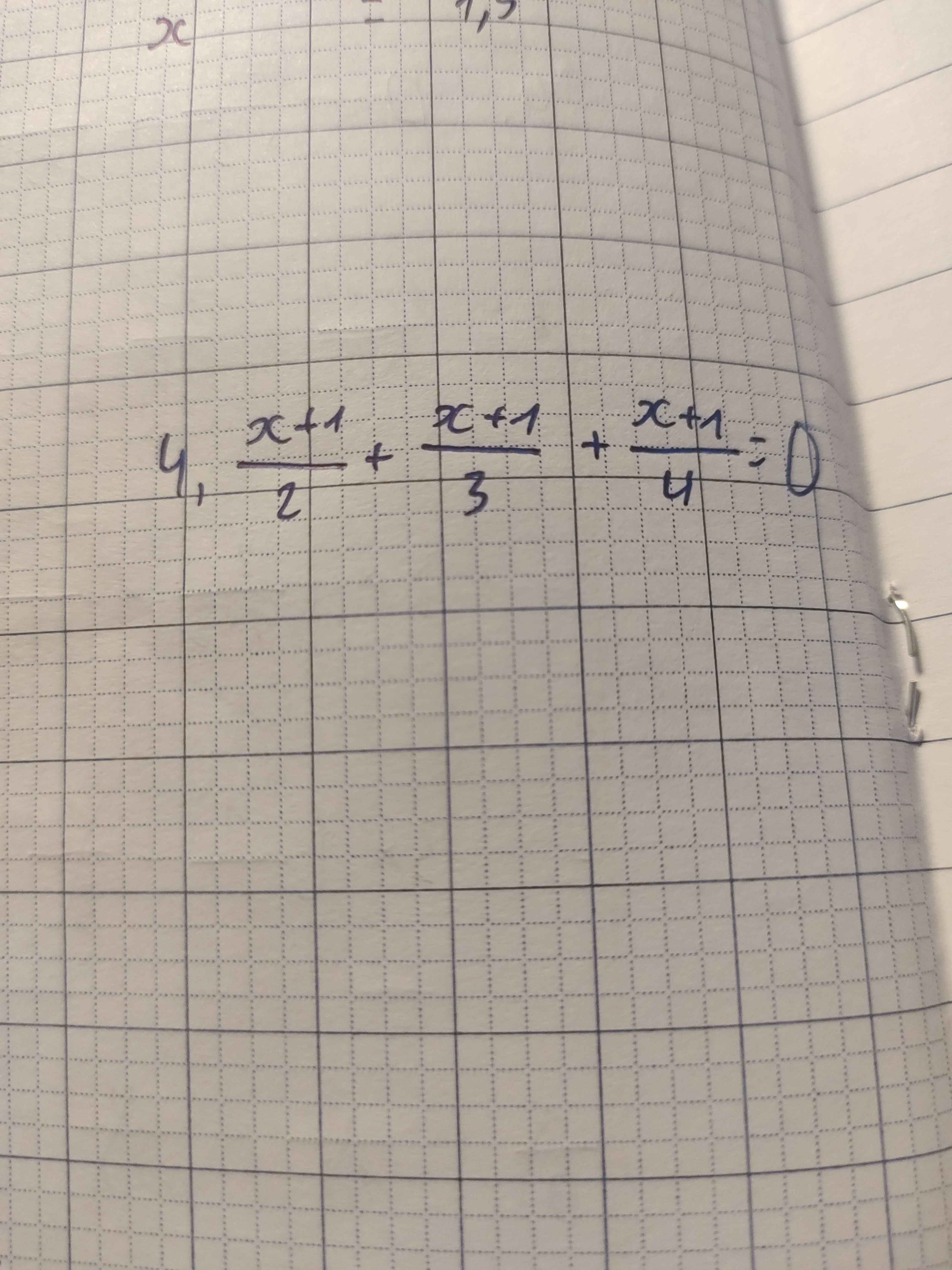 Cíu mik với
Cíu mik với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


câu b đề bài cho B < \(\dfrac{1}{3}\) thì cần gì chứng minh nữa em.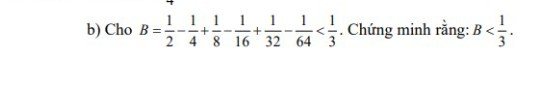
Đáng lẽ phải là: Cho B = \(\dfrac{1}{2}\) - \(\dfrac{1}{4}\) +...-\(\dfrac{1}{64}\)
Chứng minh B < \(\dfrac{1}{3}\)

Tính rồi so sánh kết quả
a) 23 : 0,5 = 46
23 x 2 = 46
46 = 46 => 23 : 0,5 = 23 x 2
b) 18 : 0,25 = 72
18 x 4 = 72
72 = 72 => 18 :0,25 = 18 x 4
Tính
a) 23,4 + 164 : 4,5
= 23,4 + `328/9`
= `2693/45`
b) 25,67 x 3,5 - 43,21
= 89,845 - 43,21
= 46,635

`n^2+n+4` chia hết cho n + 1
`=>(n^2+n) +4` chia hết cho n + 1
`=> n(n+1)+4` chia hết cho n + 1
Mà: `n(n+1)` chia hết cho n + 1
=> 4 chia hết cho n + 1
=> n + 1 ∈ Ư(4) = {1; -1; 2; -2; 4; -4}
=> n ∈ {0; -2; 1; -3; 3; -5}

\(\left(27+11\right)\cdot\left(512-\left[14\cdot\left(64-4^2\right):2\right]\right)\\ =33\cdot\left[512-\left[14\cdot\left(64-16\right):2\right]\right]\\ =33\cdot\left(512-14\cdot48:2\right)\\ =33\cdot\left(512-14\cdot24\right)\\ =33\cdot\left(512-336\right)\\ =33\cdot176\\ =5808\)


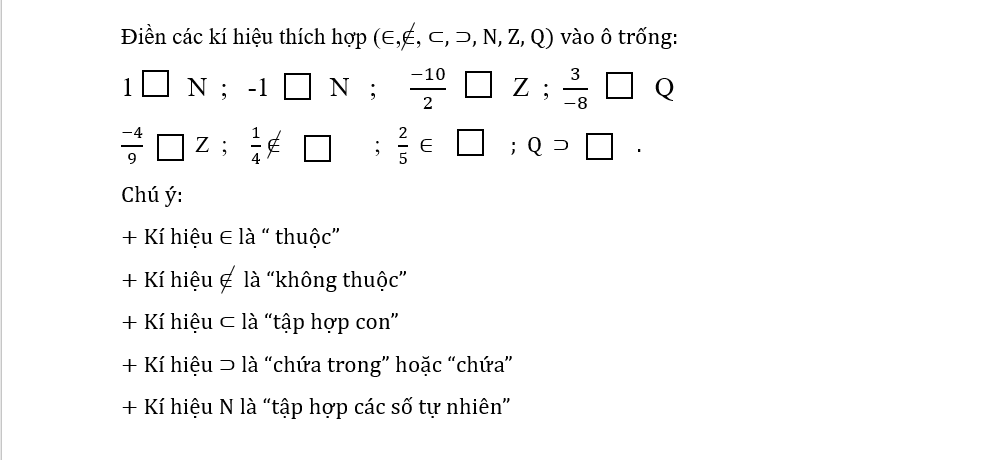
\(-4\notin N\\ -\dfrac{5}{3}\in Q\\ -8\in Q\\ -\dfrac{2}{9}\notin Z\\ -\dfrac{1}{11}\notin Z\\ -\dfrac{2}{7}\in Q\\ -\dfrac{2}{19}\notin N\\ N\subset Q\)








\(\dfrac{x+1}{2}+\dfrac{x+1}{3}+\dfrac{x+1}{4}=0\\ \dfrac{1}{2}\times\left(x+1\right)+\dfrac{1}{3}\times\left(x+1\right)+\dfrac{1}{4}\times\left(x+1\right)=0\\ \left(x+1\right)\times\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\right)=0\\ x+1=0:\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\right)\\ x+1=0\\ x=-1\)