tìm nghiệm của các đa thức sau:
A)(2x-4)*(x+9)
B)(x+1)(x-1)(3-2x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) x = 0 là nghiệm của P(x) nên:
P(0) = 0
2.0 + a - 1 = 0
a = 1
b) x = 1 là nghiệm của P(x) nên:
P(1) = 0
2.1 + a - 1 = 0
a + 1 = 0
a = -1
a) Do P(x) nhận `x=0` là nghiệm nên:
Thay `x=0` vào P(x) ta có:
\(2\cdot0+a-1=0\)
\(\Rightarrow a-1=0\)
\(\Rightarrow a=1\)
b) Do P(x) nhận `x=1` là nghiệm nên:
Thay `x=1` vào P(x) ta có:
\(2\cdot1+a-1=0\)
\(\Rightarrow2+a-1=0\)
\(\Rightarrow a+1=0\)
\(\Rightarrow a=-1\)

- Phân tử gồm 2 nguyên tử X liên kết với 1 nhóm CO3
→ CTHH: X2CO3
⇒ 2MX + 60 = 106
⇒ MX = 23
→ X là Na

3x(12x – 4) – 9x(4x – 3) = 30
3x.12x – 3x.4 – (9x.4x – 9x.3) = 30
36x2 – 12x – 36x2 + 27x = 30
(36x2 – 36x2) + (27x – 12x) = 30
15x = 30
x = 2
Vậy x = 2.
Chúc bạn học tốt, tick cho tui nhoe

Nhân vật thuyền trưởng Nê trong văn bản "Dòng Sông Đen Cứu Vớt Mình Cần Gấp" đem lại cho độc giả nhiều bài học quý giá, trong đó có:
Sự quyết đoán và kiên nhẫn: Thuyền trưởng Nê đã thể hiện sự quyết đoán và kiên nhẫn khi đứng đầu tàu trong những tình huống khó khăn và nguy hiểm. Anh ta không bao giờ từ bỏ trước thách thức, luôn tìm cách giải quyết vấn đề một cách sáng suốt và quyết định.
Trách nhiệm và lòng nhân hậu: Nê luôn đặt trách nhiệm lên hàng đầu và luôn chăm sóc cho toàn thể hành khách trên tàu một cách tận tâm. Anh ta có tấm lòng nhân hậu và luôn quan tâm đến người khác, không ngần ngại giúp đỡ khi cần thiết.
Sự tin tưởng và ổn định: Thuyền trưởng Nê là một người đầy niềm tin vào khả năng của bản thân và đồng đội, luôn duy trì tinh thần lạc quan và ổn định trong mọi tình huống khó khăn.
Từ những bài học trên, độc giả có thể học được lòng kiên nhẫn, trách nhiệm, lòng nhân hậu và sự tin tưởng từ nhân vật thuyền trưởng Nê, giúp em trở thành con người hoàn thiện và thành công trong cuộc sống.

a: \(10x^2-7x+a⋮2x-3\)
=>\(10x^2-15x+8x-12+a+12⋮2x-3\)
=>a+12=0
=>a=-12
b: \(2x^2+ax-4⋮x+4\)
=>\(2x^2+8x+\left(a-8\right)x+4a-32-4a+28⋮x+4\)
=>-4a+28=0
=>a=7

a: A(x)+B(x)
\(=-3x^3+5x^2+4x+1+3x^3+6x^2-8x+9\)
\(=11x^2-4x+10\)
A(x)-B(x)
\(=-3x^3+5x^2+4x+1-3x^3-6x^2+8x-9\)
\(=-6x^3-x^2+12x-8\)
b: C(x)+D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}+4x^3-5x^2-3x-\dfrac{1}{4}\)
\(=3x^3+2x-1\)
C(x)-D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}-4x^3+5x^2+3x+\dfrac{1}{4}\)
\(=-5x^3+10x^2+8x-\dfrac{1}{2}\)
c: E(x)+F(x)
\(=3x^3+7x^2+5x-8+3x^3+7x^2-9x+1\)
\(=6x^3+14x^2-4x-7\)
E(x)-F(x)
\(=3x^3+7x^2+5x-8-3x^3-7x^2+9x-1\)
\(=14x-9\)
d: G(x)+H(x)
\(=5x^4-6x^3-3x^2-2x+8+x^4+3x^2-3x-5\)
\(=6x^4-6x^3-5x+3\)
G(x)-H(x)
\(=5x^4-6x^3-3x^2-2x+8-x^4-3x^2+3x+5\)
\(=4x^4-6x^3-6x^2+x+13\)
e: I(x)+J(x)
\(=5x^4-2x^3-6x^2+7x+6+2x^3+3x^2-7x-5\)
\(=5x^4-3x^2+1\)
I(x)-J(x)
\(=5x^4-2x^3-6x^2+7x+6-2x^3-3x^2+7x+5\)
\(=5x^4-4x^3-9x^2+14x+11\)
f: K(x)+L(x)
\(=4x^4+3x^3+5x^2-2x+6-4x^4-3x^3-4x^2+2x-9\)
\(=x^2-3\)
K(x)-L(x)
\(=4x^4+3x^3+5x^2-2x+6+4x^4+3x^3+4x^2-2x+9\)
\(=8x^4+6x^3+9x^2-4x+15\)
g: M(x)+N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19+6x^4-4x^3+3x^2+\dfrac{1}{2}x-20\)
\(=x^4-2x^2-39\)
M(x)-N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19-6x^4+4x^3-3x^2-\dfrac{1}{2}x+20\)
\(=-11x^4+8x^3-8x^2-x+1\)
h:
\(O\left(x\right)=x^5+x^3-4x-x^5+3x+7\)
\(=\left(x^5-x^5\right)+x^3+\left(-4x+3x\right)+7\)
\(=x^3-x+7\)
\(P\left(x\right)=3x^2-x^3+8x-3x^2-14\)
\(=-x^3+\left(3x^2-3x^2\right)+8x-14=-x^3+8x-14\)
O(x)+P(x)
\(=x^3-x+7-x^3+8x-14\)
\(=7x-7\)
O(x)-P(x)
\(=x^3-x+7+x^3-8x+14\)
\(=2x^3-9x+21\)

Lời giải:
Ta thấy:
$x^4\geq 0; x^2\geq 0$ với mọi $x$
$\Rightarrow Q(x)=x^4+3x^2+1\geq 1>0$ với mọi $x$
$\RIghtarrow Q(x)$ không có nghiệm với mọi $x$



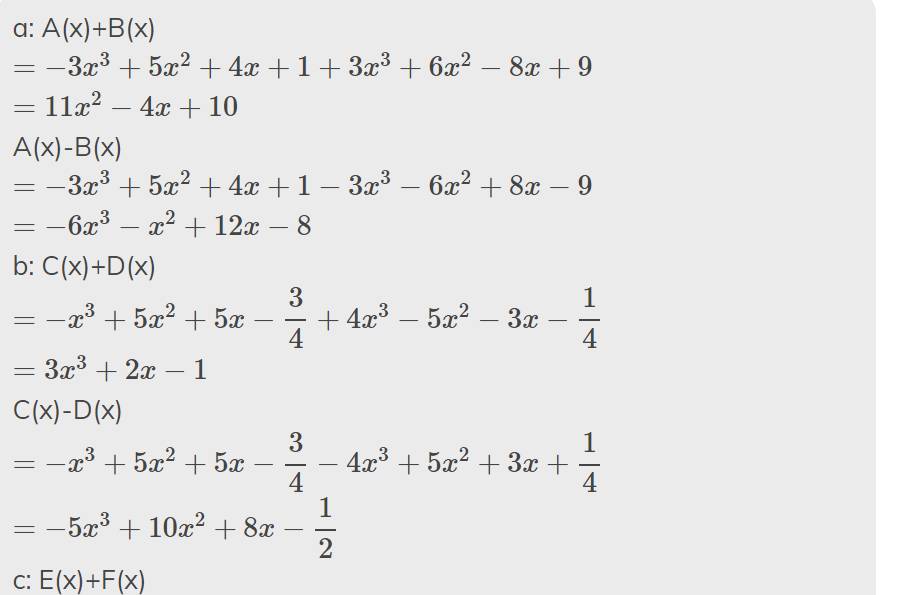

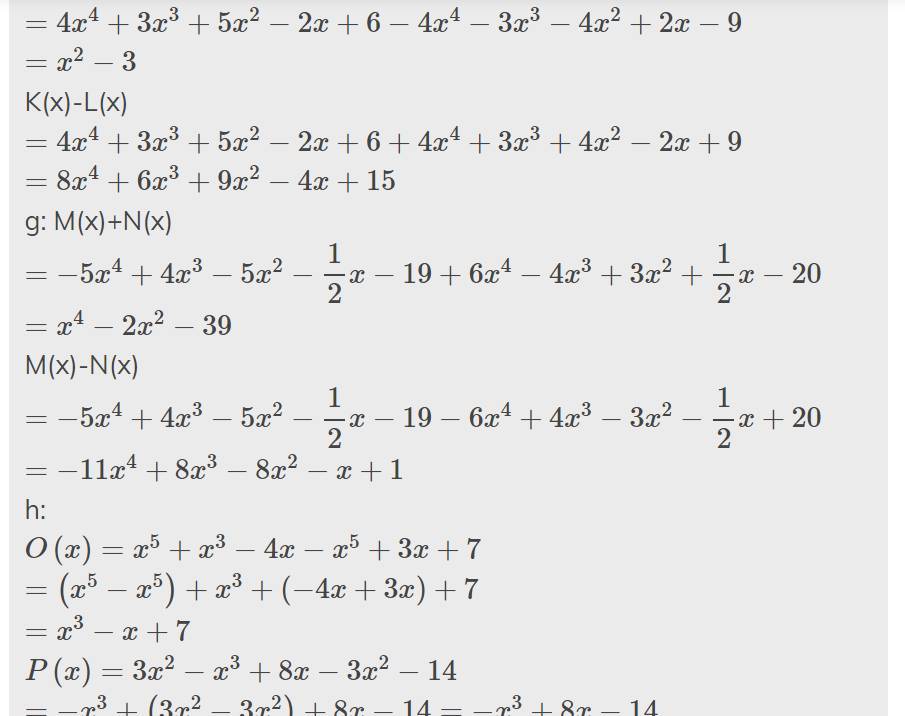
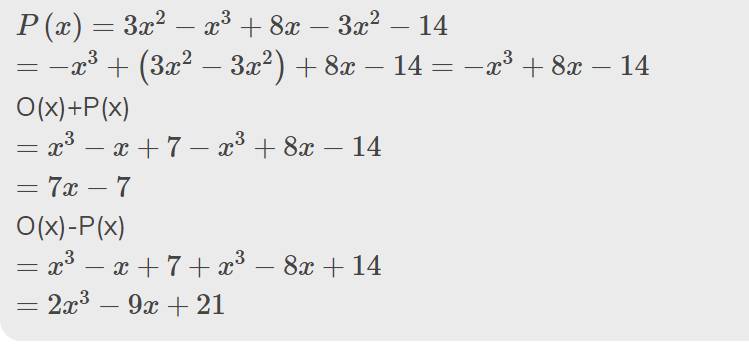
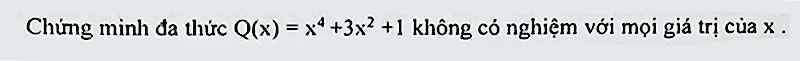
a; (2\(x-4\)).(\(x+9\)) = 0
\(\left[{}\begin{matrix}2x-4=0\\x+9=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=4\\x=-9\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=2\\x=-9\end{matrix}\right.\)
Vậy \(x\) {-9; 2}
b; (\(x\) + 1).(\(x-1\)).(3 - 2\(x\)) = 0
\(\left[{}\begin{matrix}x+1=0\\x-1=0\\3-2x=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=1\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-1; 1; \(\dfrac{3}{2}\)}