Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) PTHH: \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
b) Đặt \(n_{CH_4}=x\left(mol\right);n_{C_2H_4}=y\left(mol\right)\). Khi đó \(22,4x+22,4y=4,48\) \(\Leftrightarrow x+y=0,2\)
Từ PTHH \(\Rightarrow n_{O_2\left(1\right)}=2x\left(mol\right)\)\(;n_{O_2\left(2\right)}=3y\left(mol\right)\). Khi đó \(2x.22,4+3y.22,4=11,2\) \(\Leftrightarrow2x+3y=0,5\)
Vậy ta có \(\left\{{}\begin{matrix}x+y=0,2\\2x+3y=0,5\end{matrix}\right.\Leftrightarrow x=y=0,1\left(mol\right)\)
\(\Rightarrow\%V_{CH_4}=\%V_{C_2H_4}=50\%\)

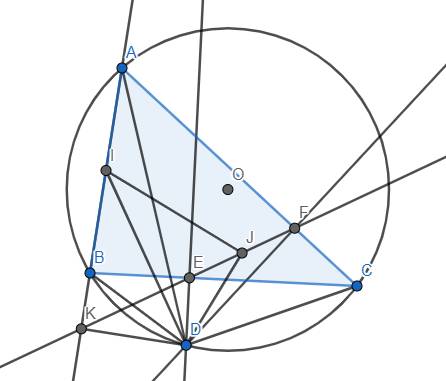
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.
b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp.
Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)
\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)
c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm

a. Để có một trận đấu ta có 5 cách chọn đội thứ nhất, 4 cách chọn đội thứ 2. Vì mỗi đội chỉ đấu với nhau 1 trận nên số trận đấu của bảng đấu là: 5 .4 : 2 = 10 trận.
b. Mỗi trận đấu tổng điểm của hai đội là 3 điểm hoặc 2 điểm
Tổng điểm tối đa của 5 đội là: 10 . 3 = 30 điểm
Tổng điểm thực tế của 5 là: 10 + 9 + 6 + 4 +0 =29 điểm
Điểm thực tế ít hơn điểm tối đa là 1 nên có 1 trận hòa.
Hai đội A và D hòa nhau, vì điểm 2 đội không chia hết cho 3.
BĐT cần chứng minh tương đương:
\(\dfrac{a}{a+\sqrt{3a+bc}}+\dfrac{b}{b+\sqrt{3b+ca}}+\dfrac{c}{c+\sqrt{3c+ab}}\le1\)
Ta có:
\(\dfrac{a}{a+\sqrt{3a+bc}}=\dfrac{a}{a+\sqrt{a\left(a+b+c\right)+bc}}=\dfrac{a}{a+\sqrt{\left(a+b\right)\left(c+a\right)}}\le\dfrac{a}{a+\sqrt{\left(\sqrt{ab}+\sqrt{ac}\right)^2}}\)
\(=\dfrac{a}{a+\sqrt{ab}+\sqrt{ac}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự:
\(\dfrac{b}{b+\sqrt{3b+ca}}\le\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\dfrac{c}{c+\sqrt{3c+ab}}\le\dfrac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng vế:
\(\dfrac{a}{a+\sqrt{3a+bc}}+\dfrac{b}{b+\sqrt{3b+ca}}+\dfrac{c}{c+\sqrt{3c+ab}}\le\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)