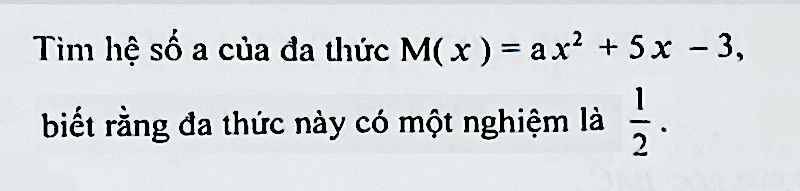
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Chỉ có 1 khả năng xuất hiện mặt có số chấm bằng 4 trong 6 khả năng nên P(A) = 1616.
b) Chỉ có 1 khả năng xuất hiện mặt có số chấm bằng 5 là số chia hết cho 5 trong 6 khả năng nên P(B) = 1616.
c) Không có mặt nào có số chấm là số tròn chục nên biến cố C là biến cố không thể.
Do đó P(C) = 0.
a:
\(\Omega=\left\{1;2;3;4;5;6\right\}\)
=>\(n\left(\Omega\right)=6\)
Gọi A là biến cố "Gieo được mặt có số chấm là 4"
=>A={4}
=>n(A)=1
=>\(P\left(A\right)=\dfrac{1}{6}\)
b: Gọi B là biến cố "Gieo được mặt có số chấm là số lẻ"
=>B={1;3;5}
=>n(B)=3
=>\(P\left(B\right)=\dfrac{3}{6}=\dfrac{1}{2}\)
c: Gọi C là biến cố "Gieo được mặt có số chấm lớn hơn 1"
=>C={2;3;4;5;6}
=>n(C)=5
\(P\left(C\right)=\dfrac{5}{6}\)

\(\left(20x^6-5x^5+15x^4\right):\left(-3x^3\right)\)
\(=20x^6:\left(-3x^3\right)+\left(-5x^5\right):\left(-3x^3\right)+15x^4:\left(-3x^3\right)\)
\(=-\dfrac{20}{3}x^{6-3}+\dfrac{5}{3}x^{5-3}-5x^{4-3}\)
\(=-\dfrac{20}{3}x^3+\dfrac{5}{3}x^2-5x\)

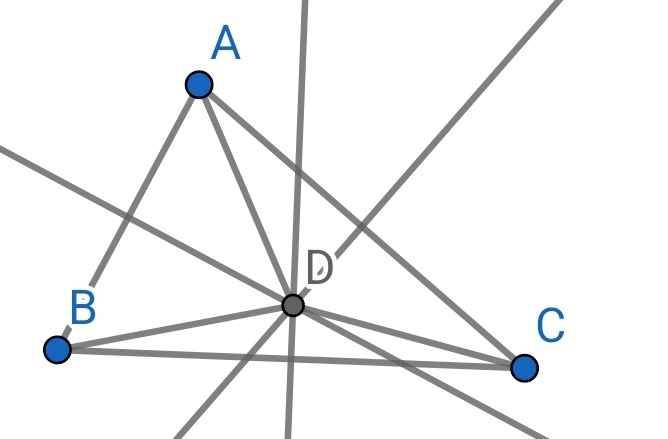
Xem vị trí 3 ngôi làng là 3 đỉnh của ∆ABC
Khi đó vị trí đặt cột thu sóng tại D, với D là giao điểm của ba đường trung trực của ∆ABC
Theo tính chất ba đường trung trực của tam giác thì điểm D cách đều ba đỉnh A, B, C

`a+b+c=2p <=> a^2+b^2+c^2+2(ab+bc+ca)=4p^2`.
`4p(p-a) = 4p^2 - 4pa = a^2+b^2+c^2+2(ab+bc+ca) - 2a(a+b+c)`
`= a^2+b^2+c^2 + 2ab+2bc+2ca-2a^2- 2ab - 2ac`
`= b^2+c^2-a^2+2bc.`


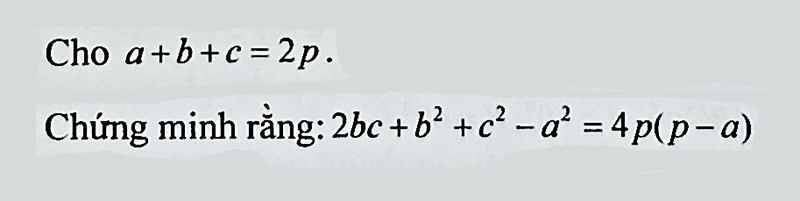
M(1/2)=0
=>\(a\cdot\left(\dfrac{1}{2}\right)^2+5\cdot\dfrac{1}{2}-3=0\)
=>\(a\cdot\dfrac{1}{4}=\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2}:\dfrac{1}{4}=2\)
Vì M(\(x\)) = a\(x^2\) + 5\(x\) - 3
M(\(\dfrac{1}{2}\)) = 0
a.(\(\dfrac{1}{2}\))2 + 5.(\(\dfrac{1}{2}\)) - 3 = 0
\(\dfrac{1}{4}\)a + \(\dfrac{5}{2}\) - 3 = 0
\(\dfrac{1}{4}\)a - \(\dfrac{1}{2}\) = 0
\(\dfrac{1}{4}\)a = \(\dfrac{1}{2}\)
a = \(\dfrac{1}{2}\) : \(\dfrac{1}{4}\)
a = 2
Vậy để \(x\) = \(\dfrac{1}{2}\) là nghiệm của đa thức thì a = 2