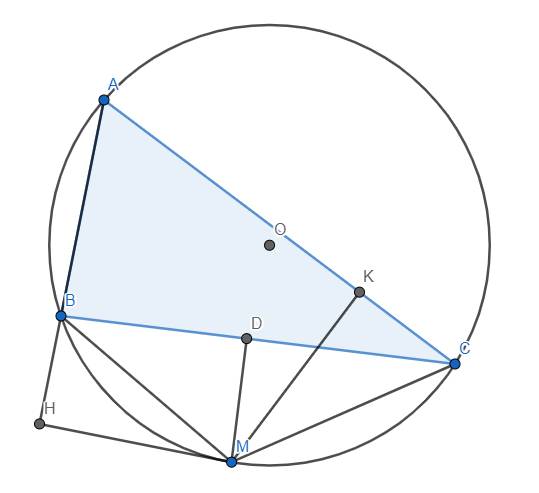
1, 2 góc bằng nhau với hai góc bằng nhau khác
2, 2 góc bằng tổng hoặc hiệu của 2 góc theo thứ tự đôi 1 bằng nhau
3, 2 góc cùng phụ nhau( hoặc cùng bù) với góc thứ 3
4, 2 góc cùng nhọn hoặc cùng tù có các cạnh đôi 1 hoặc vuông góc
5, hai góc SLT, SL ngoài, đồng vị
6, hai dây chắn giữa chúng 2 cung bằng nhau trong 1 đường tròn
7,2 cạnh đối của hình bình hành, hình chữ nhật, hình vuông
8, 2 góc bằng nhau có 1 cạnh trùng nhau
9, 3 đường phân giác trong và ngoài của góc kia
10, cạnh góc vuông đôi 1 bằng nhau
11, 2 góc bằng nhau đôi 1
12, một góc bằng nhau xen giữa 2 cạnh tương ứng tỉ lệ
13, có 3 cạnh tương ứng tỉ lệ
Mọi người vẽ hình giúp mình nhé vì mình ko hình dung được ( nếu được bạn nêu luôn cách hiểu bằng chữ nhé ), xong các bạn giải thích giúp mình " đôi một" ở trên là sao? Dù hơi dài nhưng các bạn giúp mk nha coi như là ôn thi vào 10 đi. Nó ko thừa đâu :333
THANK YOU nhé