Bài 7. Cho hình thang ABCD vuông góc tại A. Đáy AD = 2BC , đường chéo AC là phân giác A. Vẽ CE song song AB. Chứng minh ABCE là hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$A=(4x^2-4xy+y^2)+20x-10y+25$
$=(2x-y)^2+10(2x-y)+25$
$=(2x-y+5)^2\geq 0$
Vậy GTNN của $A$ là $0$. Dấu "=" xảy ra khi $2x-y+5=0$
A= (4x2 - 4xy + y2 ) + (20x -10y) + 25
A= (2x - y)2 + 10( 2x - y) +25
A= \([\)(2x - y ) + 5\(]^2\)
A luôn ≥ 0 vây A nhỏ nhất khi A = 0

Gọi \(x\) là số đồng tiền của "tôi" và \(y\) là số rương \(\left(x,y\inℕ^∗\right)\)
Khi "tôi" đặt 9 đồng tiền vào mỗi rương thì 2 rương trống rỗng, như vậy ta có \(9\left(y-2\right)=x\Leftrightarrow9y-x=18\)
Khi "tôi" đặt 6 đồng tiền vàng vào mỗi rương thì còn lại 3 đồng tiền vàng nên ta có \(6y=x-3\Leftrightarrow x=6y+3\)
Kết hợp 2 phương trình này lại, ta được phương trình \(9y-\left(6y+3\right)=18\Leftrightarrow3y=21\Leftrightarrow y=7\) (nhận)
Từ đó \(x=6y+3=6.7+3=45\) (nhận)
Vậy "tôi" có 45 đồng tiền.

a)IM là đg trung bình của △ABC → IM//AB và IM = \(\dfrac{1}{2}AB\)
mà N đối xứng với M qua I → IN = IM hay IM = 1/2 NM
⇒ AB // NM và AB = NM
⇒ ABMN là hình bình hành
O là giao điểm 2 đg chéo ⇒ ON = OB
xét △ NMB có IO là đg trung bình → IO // MB và IO = 1/2 MB
mà MB = 1/2 BC
⇒ IO = 1/4 BC hay BC = 4OI
b) thêm điều kiên là tam giác cân tại A
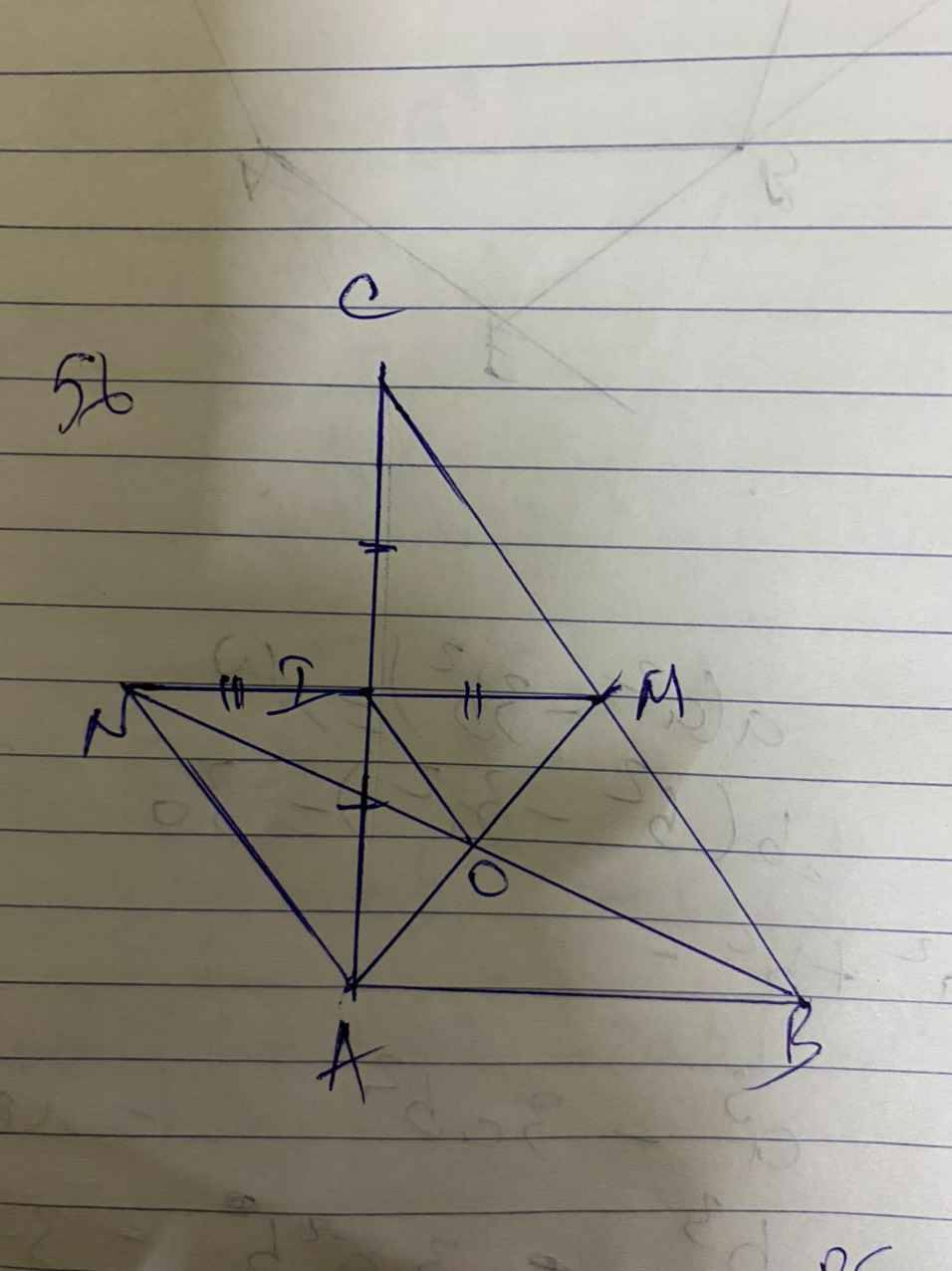

nãy gõ đáp án xong ấn nhầm nút lại bị xóa hết nên mình chụp lại - chữ xấu nha


a) =3x(x-2)
b) 2xy(1+z)
c)3x2 (5 - 3y2)
d) 3x2 (9x + x)
e) x(x-3)(2x-1)
f)(x-2y)(3x+y)
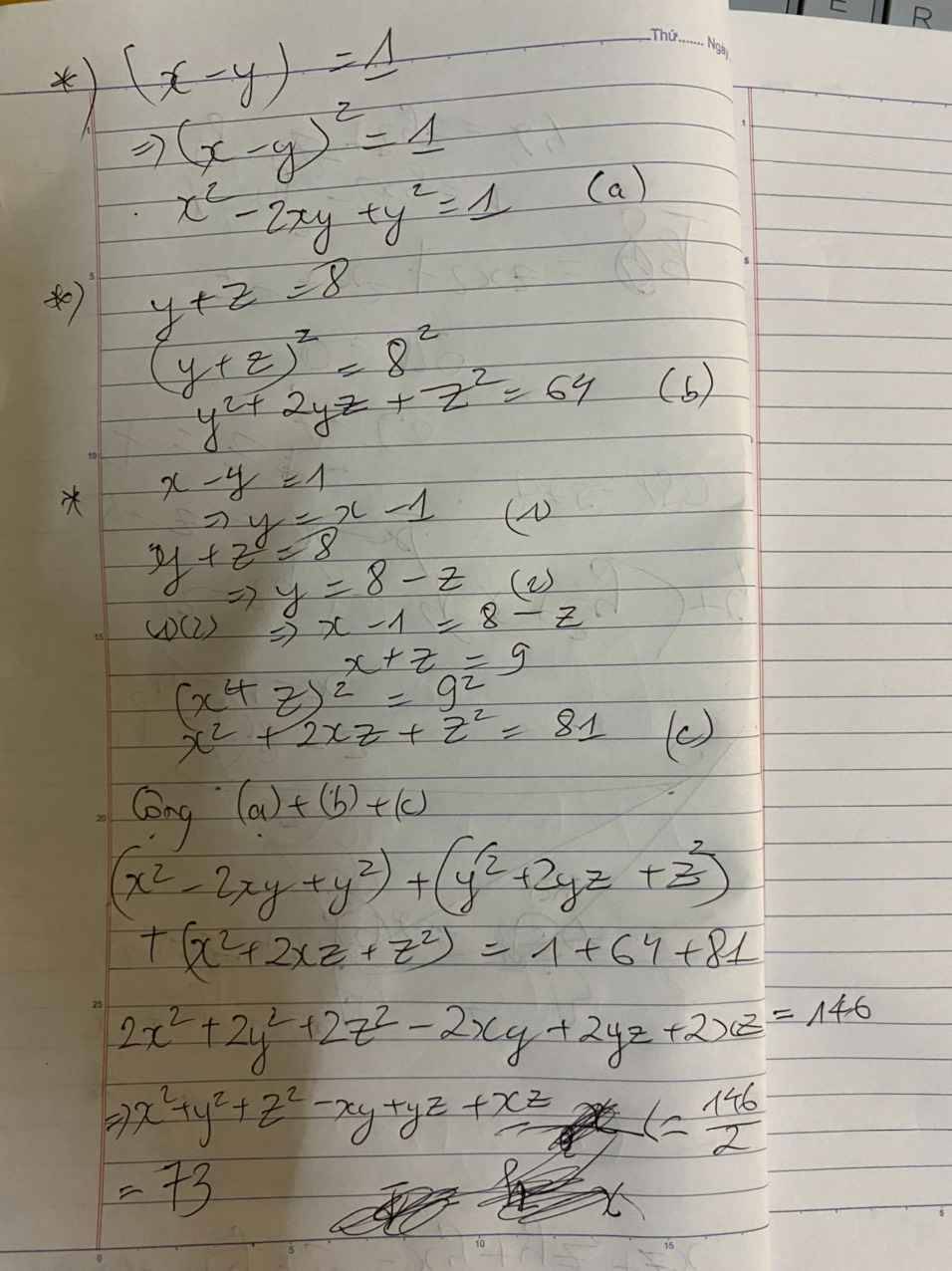
\(CE\) song song với \(AB\) nên
\(\widehat{CEA}+\widehat{BAE}=180^o\Rightarrow\widehat{CAE}=180^o-\widehat{BAE}=180^o-90^o=90^o\).
Xét tứ giác \(ABCE\) có:
\(\widehat{BAE}=\widehat{ABC}=\widehat{CEA}=90^o\) suy ra \(ABCE\) là hình chữ nhật.
Mà \(ABCE\) có \(AC\) là phân giác của góc \(A\) do đó \(ABCE\) là hình vuông.