Bài này áp dụng BĐT B.C.S là ra nhé

Ta có \(VT=\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\ge\dfrac{\left(a+b+c\right)^2}{b+c+a}=a+b+c=VP\) 

Dấu "=" xảy ra \(\Leftrightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}\Leftrightarrow a=b=c\)

(*) BĐT B.C.S phát biểu như sau:

 Cho \(2n\) số thực \(a_1,a_2,...,a_n,x_1,x_2,...,x_n\), trong đó \(a_i>0,\forall i\in\left\{1,2,...,n\right\}\). Khi đó ta có:

 \(\dfrac{x_1^2}{a_1}+\dfrac{x_2^2}{a_2}+...+\dfrac{x_n^2}{a_n}\ge\dfrac{\left(x_1+x_2+...+x_n\right)^2}{a_1+a_2+...+a_n}\) (*)

Dấu "=" xảy ra \(\Leftrightarrow\dfrac{x_1}{a_1}=\dfrac{x_2}{a_2}=...=\dfrac{x_n}{a_n}\)

Trước tiên, ta chứng minh (*) đúng với \(n=2\). Thật vậy:

Với \(x,y\inℝ;a,b>0\), thì ta cần chứng minh 

\(\dfrac{x^2}{a}+\dfrac{y^2}{b}\ge\dfrac{\left(x+y\right)^2}{a+b}\)

 \(\Leftrightarrow\dfrac{bx^2+ay^2}{ab}\ge\dfrac{\left(x+y\right)^2}{a+b}\)

\(\Leftrightarrow\left(a+b\right)\left(bx^2+ay^2\right)\ge ab\left(x+y\right)^2\)

\(\Leftrightarrow abx^2+a^2y^2+b^2x^2+aby^2\ge abx^2+aby^2+2abxy\)

\(\Leftrightarrow a^2y^2-2abxy+b^2x^2\ge0\)

\(\Leftrightarrow\left(ay-bx\right)^2\ge0\) (luôn đúng)

 Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow ay=bx\Leftrightarrow\dfrac{x}{a}=\dfrac{y}{b}\)

 Để chứng minh với \(n\ge3\) thì bạn chỉ cần dùng nhiều lần BĐT cho 2 phân thức là được.

 VD: \(\dfrac{x^2}{a}+\dfrac{y^2}{b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y\right)^2}{a+b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y+z\right)^2}{a+b+c}\)

Vậy BĐT được chứng minh.

Sửa lại đề chỗ kia là \(\dfrac{b}{a}\) chứ không phải \(\dfrac{b}{b}\) nhé.

Đặt \(\dfrac{a}{b}=t>0\) . Khi đó BĐT cần chứng minh tương đương:

\(t^2+\dfrac{1}{t^2}\ge t+\dfrac{1}{t}\) 

\(\Leftrightarrow t^2+\dfrac{1}{t^2}+2\ge t+\dfrac{1}{t}+2\)

\(\Leftrightarrow\left(t+\dfrac{1}{t}\right)^2\ge t+\dfrac{1}{t}+2\) (*)

Đặt \(u=t+\dfrac{1}{t}\left(u\ge2\right)\), khi đó (*) tương đương:

\(u^2-u-2\ge0\)

\(\Leftrightarrow u^2+u-2u-2\ge0\)

\(\Leftrightarrow u\left(u+1\right)-2\left(u+1\right)\ge0\)

\(\Leftrightarrow\left(u+1\right)\left(u-2\right)\ge0\) (luôn đúng vì \(u\ge2\))

Dấu "=" xảy ra \(\Leftrightarrow u=2\) \(\Leftrightarrow t+\dfrac{1}{t}=2\) \(\Leftrightarrow t=1\) \(\Leftrightarrow a=b\)

Vậy ta có đpcm.

 Nãy mình nhìn nhầm đề, xin lỗi bạn nhiều. Cách trình bày vẫn như vậy nhé.

Lời giải:
Vì tỉ số chiều dài và chiều rộng là $\frac{3}{7}$ nên gọi chiều dài là $a$ (m) thì chiều rộng là $\frac{3}{7}\times a$ (m) 

Diện tích: $a.\frac{3}{7}a=84$

$\Rightarrow a^2=196=14^2$

$\Rightarrow a=14$ (m) 

Vậy chiều dài là 14 m, chiều rộng là $14.\frac{3}{7}=6$ (m) 

Độ dài hàng rào bao quanh mảnh đất chính bằng chu vi mảnh đất và bằng: 
$2(14+6)=40$ (m)

Lời giải:
Chu vi đáy lăng trụ: $6+7+9=22$ (cm)

Diện tích xung quanh lăng trụ: $22.13=286$ (cm²)

a) = (\(-\dfrac{141}{20}\)- \(\dfrac{1}{4}\)) : (-5) + \(\dfrac{1}{15}\) - \(\dfrac{1}{15}\)

    = \(-\dfrac{73}{10}\) : - 5

    = \(\dfrac{73}{50}\)

b) = \(\left(\dfrac{3}{25}-\dfrac{28}{25}\right)\). \(\dfrac{7}{3}\) : \(\left(\dfrac{7}{2}-\dfrac{11}{3}.14\right)\)

    = \(-\dfrac{7}{3}\) . \(-\dfrac{6}{287}\)

    = \(\dfrac{2}{41}\)

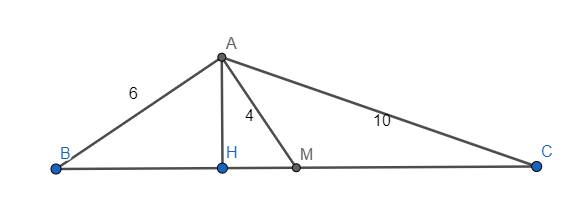
Hạ \(AH\perp BC\) tại H. Đặt \(MB=MC=x;HM=y;AH=h\)

Theo định lý Pythagoras: \(\left\{{}\begin{matrix}AH^2+HM^2=AM^2\\AH^2+BH^2=AB^2\\AH^2+CH^2=AC^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+\left(x-y\right)^2=36\\h^2+\left(x+y\right)^2=100\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+x^2+y^2-2xy=36\\h^2+x^2+y^2+2xy=100\end{matrix}\right.\)

Cộng theo vế của 2 pt thứ 2 và thứ 3 của hệ này, ta được:

\(2\left(h^2+x^2+y^2\right)=136\)

\(\Leftrightarrow x^2+\left(h^2+y^2\right)=68\)

\(\Leftrightarrow x^2+16=68\)

\(\Leftrightarrow x^2=52\) hay \(BM^2=52\)

Mà ta lại có \(AB^2+AM^2=6^2+4^2=52\)

\(\Rightarrow AB^2+AM^2=BM^2\) \(\Rightarrow\Delta ABM\) vuông tại A \(\Rightarrow\) đpcm

Gọi H là điểm đối xứng với A qua M

Xét tam giác AMB và tam giác HMC có:

\(\left\{{}\begin{matrix}HM=AM\\\widehat{AMB}=\widehat{HMC}\\MB=MC\end{matrix}\right.\)

\(\Rightarrow\Delta AMB=\Delta HMC\left(c.g.c\right)\)

\(\Rightarrow HC=AB=6cm\)

Xét tam giác HAC có:

\(AH^2+HC^2=10^2\left(8^2+6^2=10^2\right)\)

\(\Rightarrow\widehat{AHC}=90^o\)

Mà \(\Delta AMB=\Delta HMC\)

\(\Rightarrow\widehat{MAB}=\widehat{MHC}=90^o\left(đpcm\right)\)

Please

- Ta có sơ đồ: ( tự vẽ )

Chiều rộng hình chữ nhật là: 90 : ( 4 + 5 ) x 4 = 40 (m)

Chiều dài hình chữ nhật là: 90 - 40 = 50 (m)

Diện tích hình chữ nhật là: 50 x 40 = 200 (m²)

                                                  Đ/S: 200m²

Nửa chu vi của hình chữ nhật đó là:

      90:2=45(m)

-Ta có sơ đồ sau:

CD:I----I----I----I----I----I

CR:I----I----I----I----I

Chiều dài của hình chữ nhật đó là:

    45: (5+4).5=25(m)

Chiều rộng của hình chữ nhật đó là:

   45-25=20(m)

Diện tích của hình chữ nhật đó là:

  25.20=500(m²)

      Đáp số:500m²

Số liệu của đề không hiển thị. Bạn xem lại đề.

a, \(\sqrt{\left(\dfrac{x}{5}-1\right)^2}\) = \(\dfrac{4}{3}\)

             |\(\dfrac{x}{5}\) - 1| =   \(\dfrac{4}{3}\)

             \(\left[{}\begin{matrix}\dfrac{x}{5}-1=\dfrac{-4}{3}\left(x< 5\right)\\\dfrac{x}{5}-1=\dfrac{4}{3}\left(x>5\right)\end{matrix}\right.\)  

              \(\left[{}\begin{matrix}\dfrac{x}{5}=-\dfrac{1}{3}\\\dfrac{x}{5}=\dfrac{7}{3}\end{matrix}\right.\)

                \(\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=\dfrac{35}{3}\end{matrix}\right.\)

vậy \(x\) \(\in\) { - \(\dfrac{5}{3}\); \(\dfrac{35}{3}\)}

b, \(\sqrt{\left(7-x\right)\left(8+x\right)}\) = 0

        \(\left[{}\begin{matrix}7-x=0\\8+x=0\end{matrix}\right.\)

        \(\left[{}\begin{matrix}x=7\\x=-8\end{matrix}\right.\)

Vậy \(x\) \(\in\) {-8; 7}