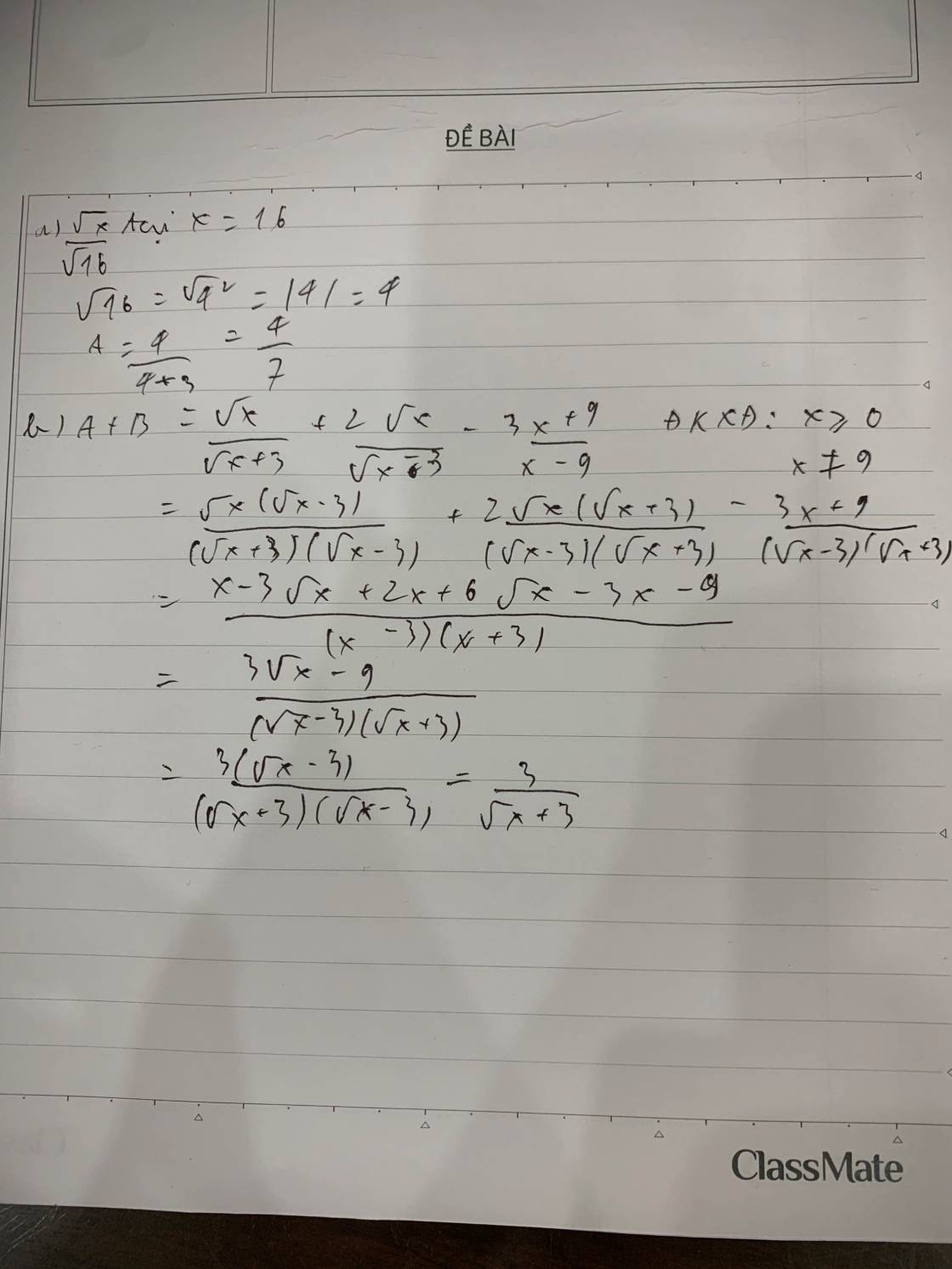
Hoành độ giao điểm (P) ; (d) tm pt 

\(x^2-2x-m+2=0\)

\(\Delta'=1-\left(-m+2\right)=m+3\)

Để (P) cắt (d) tại 2 điểm pb khi m > -3 

Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m+2\end{matrix}\right.\)

Ta có \(\left(x_1-x_2\right)^2=4\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4\)

Thay vào ta được \(4+4\left(m-2\right)=4\Leftrightarrow4m-4=4\Leftrightarrow m=2\)(tm) 

\(\left\{{}\begin{matrix}\dfrac{9}{x+1}-6y=-3\\\dfrac{10}{x+1}+6y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19}{x+1}=-19\\y=\dfrac{\dfrac{3}{x+1}+1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.\)

1, Gọi số bộ đồ tổ sản xuất phải làm mỗi ngày theo kế hoạch là x ( x ϵ N* )

Gọi số bộ đồ tổ sản xuất làm được mỗi ngày theo thực tế là x + 100 ( bộ )

Thời gian tổ sản xuất làm theo kế hoạch là \(\dfrac{4800}{x}\)( ngày ) (1)

Thời gian tổ sản xuất làm thực tế là \(\dfrac{4800}{x+100}\)( ngày ) (2)

Thực tế, tổ sản xuất đã hoàn thành trước 8 ngày nên từ (1) và (2), ta có phương trình:

\(\dfrac{4800}{x}-\dfrac{4800}{x+100}=8\)

Sau đó giải như bth là xong ^^

2) Diện tích bề mặt hình trụ là:

2πrh = 2.3,14.0,5.1,6 ≈ 5,024 ( m² )

Vậy diện tích bề mặt được sơn của thùng nước là 5,024 m²

1, Thay x = 16 vào ta được \(A=\dfrac{4}{4+3}=\dfrac{4}{7}\)

2, \(A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{-x+6\sqrt{x}-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}+3}\)

Ta có đpcm 

\(P=\sqrt{a+b}+\sqrt{b+c}\sqrt{c+a}\)

Aps dụng Bunhia-cốpxki : \(P^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)\le\left(1+1+1\right)\left(a+b+b+c+c+a\right)\)

\(=6\left(a+b+c\right)\)

\(=6.2021=12126\Leftrightarrow P=\sqrt{12126}\)

Vậy \(Max\left(P\right)=\sqrt{12126}\Leftrightarrow a=b=c=\dfrac{2021}{3}\)

(Refer ;-;)

Thể tích của phần còn lại bằng thể tích của hình trụ tròn trừ đi thể tích của phần hình nón tiện.

V(hình trụ) = πr²h =π10²20= 2000π 

V(nón) = 1/3 . πr²h(nón) =1/3 .π10². 10

V(cần tính) = V(hình trụ)  - V(nón) 

=2000π - 1000π/3

=5000π /3 (cm3)

Gọi chiều dài chiều rộng lần lượt là a ; b  ( a > b > 0 ) 

Theo bài ra ta có hệ \(\left\{{}\begin{matrix}a-b=5\\ab=750\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b+5\\b\left(b+5\right)=750\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=30\\\left[{}\begin{matrix}b=25\\b=-30\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\)

a, \(\left\{{}\begin{matrix}6x+2y=2\\x-2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1-3x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

b, đk a khác 0 

Ta có (d) // (d') <=> \(\left\{{}\begin{matrix}a=2\\b\ne-1\end{matrix}\right.\)

=> (d) : y = 2x + b ( b khác -1 ) 

(d) đi qua M(2;-3) <=> -3 = 4 + b <=> b = -7