Câu 1:

\(y=x^3+2x^2+1\)

=>\(y'=3x^2+2\cdot2x=3x^2+4x\)

\(y'\left(1\right)=3\cdot1^2+4\cdot1=3+4=7\)

Phương trình tiếp tuyến tại x=1 là:

y-f(1)=f'(1)(x-1)

=>y-4=7(x-1)

=>y=7x-7+4=7x-3

Câu 2:

a: BD\(\perp\)AC(ABCD là hình vuông)

BD\(\perp\)SA(SA\(\perp\)(ABCD))

AC,SA cùng thuộc mp(SAC)

Do đó: BD\(\perp\)(SAC)

b: \(S_{ABCD}=AB^2=a^2\)

\(V_{S.ABCD}=\dfrac{1}{3}\cdot SA\cdot S_{ABCD}=\dfrac{1}{3}\cdot3a\cdot a^2=a^3\)

a. Đúng (có nhóm -CHO)

b. Sai (Formol là chất cấm dùng trong bảo quản thực phẩm, hoa quả vì đây là chất rất độc, gây hại cho cơ thể con người chỉ với 1 lượng nhỏ)

c. Đúng

d. Đúng (aldehyde nói chung đều tham gia phản ứng tráng bạc với AgNO₃/ NH₃ để tạo kết tủa Ag màu tráng bạc)

a.

\(S_{\Delta ABC}=\dfrac{1}{2}AB.AC.sinA=\dfrac{1}{2}.a.a.sin120^0=\dfrac{a^2\sqrt{3}}{4}\)

\(\Rightarrow V=\dfrac{1}{3}SA.S_{\Delta ABC}=\dfrac{a^3}{8}\)

b.

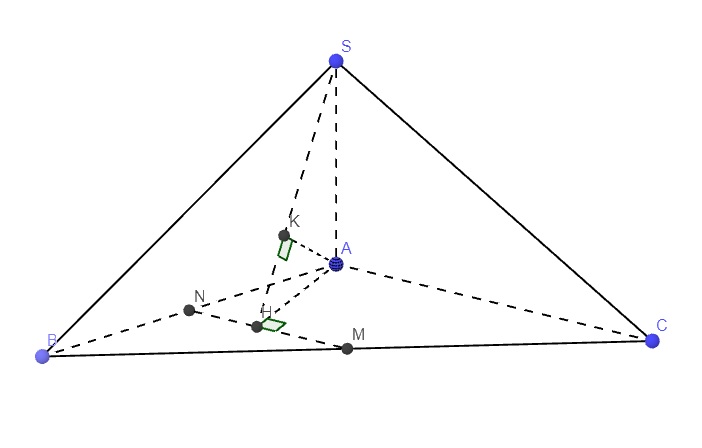
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABC

\(\Rightarrow MN||AC\Rightarrow AC||\left(SMN\right)\)

\(\Rightarrow d\left(SM;AC\right)=d\left(AC;\left(SMN\right)\right)=d\left(A;\left(SMN\right)\right)\)

Từ A kẻ AH vuông góc MN (H thuộc đường thẳng MN)

Từ A kẻ \(AK\perp SH\)  (K thuộc SH) (1)

\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp MN\\AH\perp MN\left(gt\right)\end{matrix}\right.\) \(\Rightarrow MN\perp\left(SAH\right)\)

\(\Rightarrow MN\perp AK\) (2)

(1);(2)\(\Rightarrow AK\perp\left(SMN\right)\Rightarrow AK=d\left(A;\left(SMN\right)\right)\)

AH vuông góc MN, mà AC song song MN \(\Rightarrow AH\perp AC\Rightarrow\widehat{CAH}=90^0\)

\(\Rightarrow\widehat{HAN}=\widehat{BAC}-\widehat{CAH}=120^0-90^0=30^0\)

\(\Rightarrow AH=AN.cos\widehat{HAN}=\dfrac{AB}{2}.cos30^0=\dfrac{a\sqrt{3}}{4}\)

Hệ thức lượng:

\(AK=\dfrac{AH.SA}{\sqrt{AH^2+SA^2}}=\dfrac{a\sqrt{39}}{26}\)