Tìm cặp số nguyên x y biết:
5x+3y=7
3x-5y=1
-4x+7y+13=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`[6.(-1/3)^3 -3.(-1/3)+1]:(-1/3-1)`
`= [6.((-1)^3)/(3^3)-(-3/3)+1]:(-1/3-3/3)`
`= [6. (-1/27) + 1+1]:(-4/3)`
`= [(-6/27) + (1+1)] . (-3/4)`
`= [-2/9 + 2] . (-3/4)`
`= [-2/9 + 18/9] . (-3/4)`
`= 16/9 . (-3/4)`
`= -4/3`
\(\left[6\left(-\dfrac{1}{3}\right)^3-3\cdot\left(-\dfrac{1}{3}\right)+1\right]:\left(-\dfrac{1}{3}-1\right)\)
\(=\left[6\cdot\dfrac{-1}{27}+1+1\right]:\dfrac{-4}{3}\)
\(=\left(-\dfrac{2}{9}+2\right):\dfrac{-4}{3}=\dfrac{16}{9}\cdot\dfrac{3}{-4}=\dfrac{-48}{36}=-\dfrac{4}{3}\)

Bài giải
a. Số tiền cả gốc và lãi của mẹ bạn Long rút ra khi hết kì hạn 1 năm là:
( 30000 x 5.3 : 100 ) + 30000 = 31590 ( triệu đồng )
b. Giá của chiếc xe đạp có số tiền là :
31590 x 5 : 90 = 1755 ( triệu đồng )
Đáp số : a là 31590 triệu đồng
b là 1755 triệu đồng
Cho mình hỏi tí bạn có sai đề không mà mẹ Long gửi ngận hàng 30000 triệu tức 30 ngàn tỉ dữ vậy =0 với lại vẫn còn nghỉ hè mà bạn kiểm tra cái gì dọ ?

M-N
=5x-5y-5(x-y)+2
=5(x-y)-5(x-y)+2
=2
=>Hiệu của M và N không phụ thuộc vào hai biến x,y

\(\dfrac{6^{13}-3\cdot6^{12}+3^{13}}{9^5\left(4^6+1\right)}\)
\(=\dfrac{2^{13}\cdot3^{13}-2^{12}\cdot3^{13}+3^{13}}{3^{10}\left(2^{12}+1\right)}\)
\(=\dfrac{3^{12}\left(2^{13}-2^{12}+1\right)}{3^{10}\left(2^{12}+1\right)}=\dfrac{3^2\cdot\left[2^{12}\left(2-1\right)+1\right]}{2^{12}+1}\)
\(=\dfrac{9\left(2^{12}+1\right)}{2^{12}+1}\)
=9

\(\left|x\right|=\left|y\right|\) và \(x>0;y< 0\)
\(\Rightarrow y=-x\)
\(\Rightarrow2x\pm x=x\)
Vậy \(2x+y=x\)

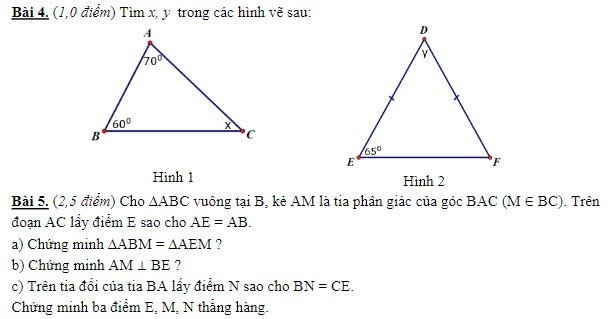
Bài 4
Hình 1: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(x+70^0+60^0=180^0\)
=>\(x=50^0\)
Hình 2: Xét ΔDEF có DE=DF
nên ΔDEF cân tại D
=>\(\widehat{EDF}=180^0-2\cdot\widehat{DEF}\)
=>\(y=180^0-2\cdot65^0=50^0\)
Bài 5:
a: Xét ΔABM và ΔAEM có
AB=AE
\(\widehat{BAM}=\widehat{EAM}\)
AM chung
Do đó: ΔABM=ΔAEM
b: ΔABM=ΔAEM
=>MB=ME
=>M nằm trên đường trung trực của BE(1)
Ta có: AB=AE
=>A nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra AM là đường trung trực của BE
=>AM\(\perp\)BE
c: Xét ΔMBN vuông tại B và ΔMEC vuông tại E có
MB=ME
BM=EC
Do đó: ΔMBN=ΔMEC
=>\(\widehat{BMN}=\widehat{EMC}\)
mà \(\widehat{EMC}+\widehat{EMB}=180^0\)(hai góc kề bù)
nên \(\widehat{BMN}+\widehat{BME}=180^0\)
=>E,M,N thẳng hàng

\(\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)...\left(\dfrac{1}{2009}-1\right)\\ =\left(\dfrac{1}{2}-\dfrac{2}{2}\right)\left(\dfrac{1}{3}-\dfrac{3}{3}\right)...\left(\dfrac{1}{2009}-\dfrac{2009}{2009}\right)\\ =\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\dfrac{-2008}{2009}\\ =\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2008}{2009}\\ =\dfrac{2\cdot3\cdot...\cdot2008}{\left(2\cdot3\cdot...\cdot2008\right)\cdot2009}\\ =\dfrac{1}{2009}\)

\(\left(\dfrac{-5}{7}\right).\left(\dfrac{2}{5}-x\right)+\dfrac{-1}{3}=\dfrac{1}{5}+\dfrac{-3}{10}\\ \Rightarrow-\dfrac{5}{7}\cdot\dfrac{2}{5}+\dfrac{5}{7}\cdot x-\dfrac{1}{3}=\dfrac{1}{5}-\dfrac{3}{10}\\ \Rightarrow-\dfrac{2}{7}+\dfrac{5}{7}x-\dfrac{1}{3}=-\dfrac{1}{10}\\ \Rightarrow-\dfrac{13}{21}+\dfrac{5}{7}x=-\dfrac{1}{10}\\ \Rightarrow\left(\dfrac{5}{7}x\right)=-\dfrac{1}{10}+\dfrac{13}{21}\\ \Rightarrow\left(\dfrac{5}{7}x\right)=\dfrac{109}{210}\\ \Rightarrow x=\dfrac{109}{150}\)
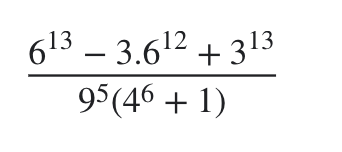
-4x+7y+13=0 chuyển thành 4x-7y=13
5x+3y=7 nhân hai vế với 4 ta có 20x+12y=28
3x-5y+4x-7y=13+1=14
7x-12y=14
20x+12y+7x-12y=42
27x=42
x=42/27 ( loại vì x là số nguyên )
vậy ko có x,y nào thoả mãn
(nếu mình sai thì cho mình xin lỗi nha)
hi