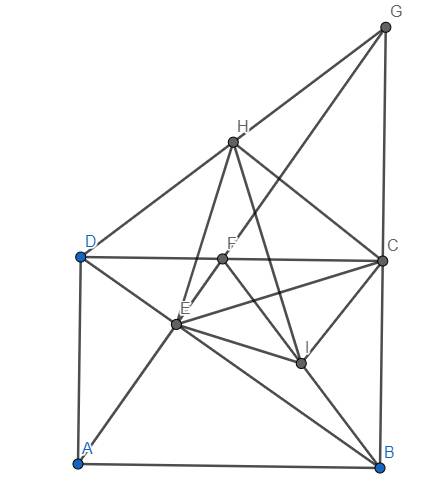
Cho hình chữ nhật ABCD (AB > AD). Vẽ AE vuông góc với BD tại E.
a) CMR: ΔABE∼ΔDBA và AB^= BE. BD
b) Giả sử AE cắt BC, DC tại G và F. CMR EA^2 = EG. EF
c) Gọi I và H lần lượt là các trung điểm của BF và DG. CMR IH ⊥ EC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

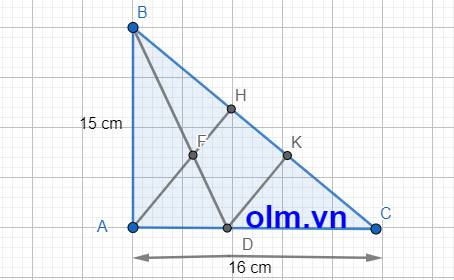
a, Xét \(\Delta\)BAH và \(\Delta\)BCA có: \(\widehat{ABC}\) chung; \(\widehat{AHB}\) = \(\widehat{BAC}\) = 900
⇒\(\Delta\)BAH \(\sim\)\(\Delta\)BCA (g-g)
⇒\(\dfrac{BA}{BC}=\dfrac{AH}{CA}=\dfrac{BH}{BA}\)
b, Theo pytago ta có: BC2 = AB2 + AC2 = 152+162 = 481 (cm2)
⇒ BC = \(\sqrt{481}\) cm
Kẻ đường cao DK vuông góc với BC cắt BC tại K
DA = DK ( vì mọi điểm trên tia phân giác thì cách đều hai cạnh còn lại)
Vì \(\Delta\)ABD và \(\Delta\)BCD có đường cao bằng nhau nên tỉ số diện tich hai tam giác bằng tỉ số hai cạnh đáy và bằng:
\(\dfrac{AB}{BC}\) = \(\dfrac{15}{\sqrt{481}}\)
Tương tự ta có tỉ số diện tích hai tam giác, tam giác ABD và tam giác BCD bằng:
\(\dfrac{AD}{DC}\) ⇒ \(\dfrac{AD}{DC}\) = \(\dfrac{15}{\sqrt{481}}\) ⇒ \(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\) = \(\dfrac{AD+DC}{15+\sqrt{481}}\) = \(\dfrac{16}{15+\sqrt{481}}\)
AD = \(\dfrac{16}{15+\sqrt{481}}\)\(\times\)15 = \(\dfrac{240}{15+\sqrt{481}}\) = \(\dfrac{15}{16}\)(\(\sqrt{481}\) - 15)
DC = \(\dfrac{16}{15+\sqrt{481}}\) \(\times\) \(\sqrt{481}\) = \(\dfrac{1}{16}\)(481 - 15\(\sqrt{481}\))

Đổi 120 000 l = 120 m3
Chiều cao của hồ nước cũng chính là độ sâu của hồ và bằng:
120 : ( 8 \(\times\) 3) = 5 (m)
Kết luận chiều sâu của hồ nước là 5m

\(\dfrac{2x}{5}=\dfrac{y}{3}\) ⇒ \(\dfrac{2x}{5}\) \(\times\) \(\dfrac{1}{2}\) = \(\dfrac{y}{3}\) \(\times\) \(\dfrac{1}{2}\) \(\Rightarrow\) \(\dfrac{x}{5}\) = \(\dfrac{y}{6}\) ⇒ \(\dfrac{x}{5}\) = \(\dfrac{3y}{18}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}\) = \(\dfrac{3y}{18}\) = \(\dfrac{x+3y}{5+18}\) = \(\dfrac{20}{23}\)
\(x\) = \(\dfrac{20}{23}\) \(\times\) 5 = \(\dfrac{100}{23}\); \(y\) = \(\dfrac{20}{23}\) : \(\dfrac{3}{18}\) = \(\dfrac{120}{23}\)
Kết luận: \(x\) = \(\dfrac{100}{23}\) và \(y\) = \(\dfrac{120}{23}\)

A B F E D H C
a/
H là trực tâm của tg ABC
\(\Rightarrow AH\perp BC\) (Trong tg 3 đường cao đồng quy tại 1 điểm)
b/
Xét 2 tg vuông ACD và tg vuông BCE có
\(\widehat{ACB}\) chung => tg ACD đồng dạng với tg BCE
\(\Rightarrow\dfrac{CD}{CE}=\dfrac{CA}{CB}\Rightarrow CE.CA=CD.CB\)

a) 3x⁵ + 4x
Cho 3x⁵ + 4x = 0
x(3x⁴ + 4) = 0
x = 0 hoặc 3x⁴ + 4 = 0 (vô lý)
Vậy nghiệm của đa thức là x = 0
b) 9x¹⁰ - 7x⁹
Cho 9x¹⁰ - 7x⁹ = 0
x⁹(9x - 7) = 0
x⁹ = 0 hoặc 9x - 7 = 0
*) x⁹ = 0
x = 0
*) 9x - 7 = 0
9x = 7
x = 7/9
Vậy nghiệm của đa thức là x = 0; x = 7/9
c) x¹⁰⁰ - x⁹⁸
Cho x¹⁰⁰ - x⁹⁸ = 0
x⁹⁸(x² - 1) = 0
x⁹⁸ = 0 hoặc x² - 1 = 0
*) x⁹⁸ = 0
x = 0
*) x² - 1 = 0
x² = 1
x = 1 hoặc x = -1
Vậy nghiệm của đa thức là x = -1; x = 0; x = 1
e) Cho 2x²(3x - 2) + x(3x - 2) = 0
(3x - 2)(2x² + x) = 0
x(3x - 2)(2x + 1) = 0
x = 0 hoặc 3x - 2 = 0 hoặc 2x + 1 = 0
*) 3x - 2 = 0
3x = 2
x = 2/3
*) 2x + 1 = 0
2x = -1
x = -1/2
Vậy nghiệm của đa thức là x = -1/2; x = 0; x = 2/3
f) Cho (1 - x)(3 - x) - (1 - x)(3 + 2x) = 0
(1 - x)(3 - x - 3 - 2x) = 0
(1 - x)(-3x) = 0
-3x = 0 hoặc 1 - x = 0
*) -3x = 0
x = 0
*) 1 - x = 0
x = 1
Vậy nghiệm của đa thức là x = 0; x = 1
g) Cho 3(3 - x) + 1/3 (3 - x)² = 0
(3 - x)[3 + 1/3 (3 - x)] = 0
(3 - x)(3 + 1 - x/3) = 0
(3 - x)(4 - x/3) = 0
3 - x = 0 hoặc 4 - x/3 = 0
*) 3 - x = 0
x = 3
*) 4 - x/3 = 0
x/3 = 4
x = 12
Vậy nghiệm của đa thức là x = 3; x = 12
h) Cho x³ + x² + x + 1 = 0
(x³ + x²) + (x + 1) = 0
x²(x + 1) + (x + 1) = 0
(x + 1)(x² + 1) = 0
x + 1 = 0 hoặc x² + 1 = 0
*) x + 1 = 0
x = -1
*) x² + 1 = 0 (vô lý)
Vậy nghiệm của đa thức là x = -1

`@` `\text {Ans}`
`\downarrow`
\(9x^{10}-7x^9=0\)
`\Leftrightarrow x^9(9x-7)=0`
`\Leftrightarrow `\(\left[{}\begin{matrix}x^9=0\\9x-7=0\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\9x=7\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\x=\dfrac{7}{9}\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x \in {0; 7/9}.`
F(\(x\)) = 9\(x^{10}\) - 7\(x^9\)
Nghiệm của F(\(x\)) là giá trị của \(x\) thỏa mãn F(\(x\)) = 0
⇔ 9\(x^{10}\) - 7\(x^9\) = 0
⇒ \(x^9\)\(\times\)(9\(x\) - 7) = 0
⇒ \(\left[{}\begin{matrix}x^9=0\\9x-7=0\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=0\\9x=7\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=0\\x=\dfrac{7}{9}\end{matrix}\right.\)
Vậy nghiệm của 9\(x^{10}\) - 7\(x^9\) là : \(x\) \(\in\){0 ; \(\dfrac{7}{9}\)}

1.
$=153^2+2.47.153+47^2=(153+47)^2=200^2=40000$
2.
$=1,24^2-2.1,24.0,24+0,24^2=(1,24-0,24)^2=1^2=1$
3. Không phù hợp để tính nhanh
4.
$=15^8-(15^8-1)=1$
5.
$=(1^2-2^2)+(3^2-4^2)+(5^2-6^2)+...+(2019^2-2020^2)$
$=(1-2)(1+2)+(3-4)(3+4)+(5-6)(5+6)+...+(2019-2020)(2019+2020)$
$=(-1)(1+2)+(-1)(3+4)+(-1)(5+6)+....+(-1)(2019+2020)$
$=(-1)(1+2+3+4+....+2019+2020)=(-1).2020(2020+1):2=-2041210$
6:
\(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =1.\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^4-1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^8-1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^{2020}-1\right)\left(2^{2020}+1\right)+1\\ =2^{4040}-1+1=2^{4040}\)

a) Ý 1: Dựa vào \(\widehat{AEB}=\widehat{DAB}=90^o\) và \(\widehat{ABD}\) chung, suy ra \(\Delta ABE~\Delta DBA\left(g.g\right)\)
Ý 2: Từ \(\Delta ABE~\Delta DBA\Rightarrow\dfrac{AB}{BD}=\dfrac{BE}{AB}\Rightarrow AB^2=BE.BD\)
b) Dễ thấy \(\widehat{DEF}=\widehat{BEG}=90^o\) và \(\widehat{DFE}=\widehat{EBG}\) (vì cùng phụ với \(\widehat{BDC}\)) nên suy ra \(\Delta EDF~\Delta EGB\left(g.g\right)\) \(\Rightarrow\dfrac{ED}{EG}=\dfrac{EF}{EB}\) \(\Rightarrow EG.EF=ED.EB\) (1)
Mặt khác, dễ dàng cm \(\Delta EAD~\Delta EBA\left(g.g\right)\) \(\Rightarrow\dfrac{EA}{EB}=\dfrac{ED}{EA}\) \(\Rightarrow EA^2=EB.ED\) (2)
Từ (1) và (2) \(\Rightarrow EA^2=EG.EF\left(=EB.ED\right)\)
c) Dễ thấy F là trực tâm của \(\Delta GBD\). \(\Delta GED\) vuông tại E có trung tuyến EH nên \(EH=\dfrac{1}{2}DG\). Tương tự suy ra \(CH=\dfrac{1}{2}DG\). Từ đó \(EH=DH\). Suy ra H nằm trên đường trung trực của đoạn CE (3)
Mặt khác, \(\Delta EBF\) vuông tại E có trung tuyến EI nên \(EI=\dfrac{1}{2}BF\). Tương tự, ta có \(CI=\dfrac{1}{2}BF\). Do đó \(EI=CI\) hay I nằm trên đường trung trực của đoạn CE (4)
Từ (3) và (4), suy ra HI là đường trung trực của đoạn CE, suy ra \(HI\perp CE\) (đpcm)
Hình vẽ đây nhé