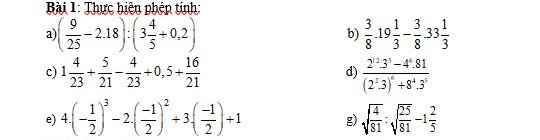
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
b) Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ BD = CD (hai cạnh tương ứng)
⇒ D là trung điểm của BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
c) Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)

a.
Xét ΔMNP có:
MN > MP (16 cm > 7 cm)
MPN là góc đối diện cạnh MN
MNP là góc đối diện cạnh MP
=> P > N (QH giữa góc và cạnh đối diện).
b.
Xét góc ngoài Δ đỉnh P
=> 180o - P
mà P > N (cmt)
=> 180o - N > 180o - P
=> góc ngoài đỉnh N > góc ngoài đỉnh P
Chúc Bạn Học Tốt ❤

Bài 5
P(x) + Q(x) = (2x³ - x² + 5x - 7) + (x³ + 3x² - 4x + 1)
= 2x³ - x² + 5x - 7 + x³ + 3x² - 4x + 1
= (2x³ + x³) + (-x² + 3x²) + (5x - 4x) + (-7 + 1)
= 3x³ + 2x² + x - 6
--------
P(x) - Q(x) = (2x³ - x² + 5x - 7) - (x³ + 3x² - 4x + 1)
= 2x³ - x² + 5x - 7 - x³ - 3x² + 4x - 1
= (2x³ - x³) + (-x² - 3x²) + (5x + 4x) + (-7 - 1)
= x³ - 4x² + 9x - 8
--------
Tại x = 2
Q(2) = 2³ + 3.2² - 4.2 + 1
= 8 + 12 - 8 + 1
= 13

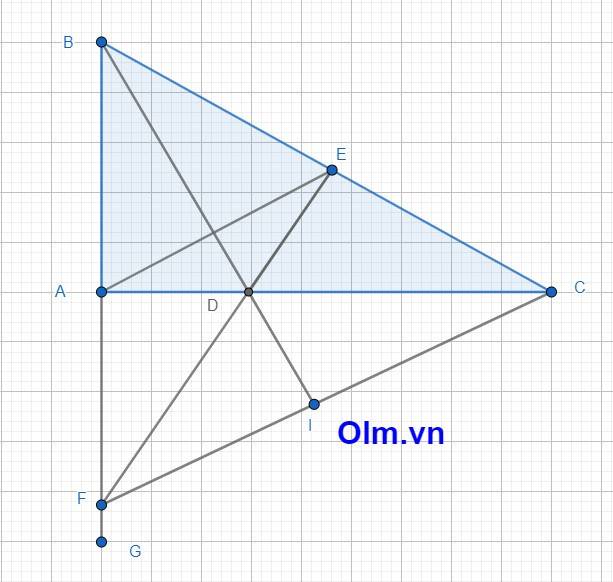
a; Xét tam giác ABD và tam giác EBD có:
\(\widehat{ABD}\) = \(\widehat{EBD}\) (vì BD là phân giác góc ABC)
AB = BE (gt)
Cạnh BD chung
⇒ \(\Delta\)ABD = \(\Delta\)EBD (c-g-c)
⇒\(\widehat{BED}\) = \(\widehat{BAD}\) = 900
⇒DE \(\perp\) BC
b; Xét tam giác BEF và tam giác ABC có:
\(\widehat{BAC}\) = \(\widehat{BEF}\) = 900
AB = BE (gt)
\(\widehat{ABE}\) chung
⇒ \(\Delta\)FBE = \(\Delta\)CBA (g-c-g)
⇒ BC = BF
BC = BE + EC = AB + AF
⇒ AF = EC
c; Xét tam giác BCF có BC = BF (cmt)
⇒ \(\Delta\)BCF cân tại B
BD là phân giác của góc B ⇒ BD là trung tuyến tam giác BCF
⇒BD \(\equiv\) BI ⇒ B;D;I thẳng hằng (vì qua một đỉnh chỉ kẻ được một đường trung tuyến của tam giác)
d; \(\widehat{AEB}\) = \(\widehat{EAC}\) + \(\widehat{ECA}\) (góc ngoài của tam giác bằng hai góc trong không kề với nó)
Xét tam giác ABE có: AB = BE (gt)
⇒ \(\Delta\)ABE cân tại B
⇒ \(\widehat{BAE}\) = \(\widehat{AEB}\) = \(\widehat{EAC}\) + \(\widehat{ECA}\) (đpcm)
Bài 1: Thực hiện phép tính:
a; (\(\dfrac{9}{25}\) - 2.18): (3\(\dfrac{4}{5}\) + 0,2)
= (0,36 - 36): (3,8 + 0,2)
= - 35,64 : 4
= - 8,91
b; \(\dfrac{3}{8}\).19.\(\dfrac{1}{3}\) - \(\dfrac{3}{8}\).33.\(\dfrac{1}{3}\)
= \(\dfrac{3}{8}\).(19\(\dfrac{1}{3}\) - 33\(\dfrac{1}{3}\))
= \(\dfrac{3}{8}\).(19 + \(\dfrac{1}{3}\) - 33 - \(\dfrac{1}{3}\))
= \(\dfrac{3}{8}\).(-14)
= - \(\dfrac{21}{4}\)